- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: How are Gamma-Poisson Distribution Fit Parameters Determined? They differ f...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
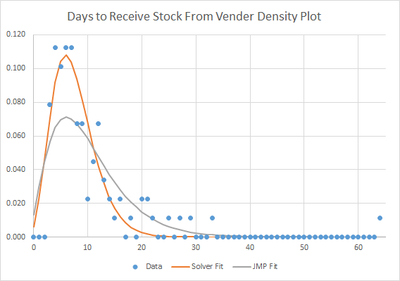
How are Gamma-Poisson Distribution Fit Parameters Determined? They differ from a least-squares solution.
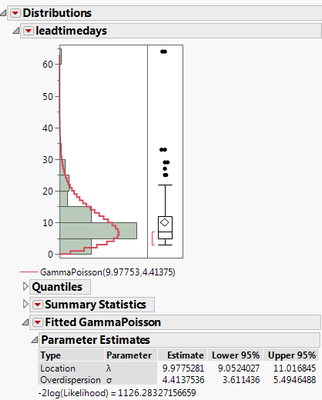
The distribution platform estimates lambda and sigma parameters for a Gamma-Poisson distribution of the attached data to be 10.0 and 4.4. A separate least-squares method finds 7.5 and 2.1. I am not proposing the orange line to be better than the gray (JMP) only that it fits my current needs better. For other data sets the parameters found by both systems are fairly close.
Does anyone have an idea as to what is happening here?
Sum of error squared
JMP: 0.014
Solver: 0.0086
Thanks,
Isaac
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How are Gamma-Poisson Distribution Fit Parameters Determined? They differ from a least-squares
normaly with MLE (maximum likelihood estimation)
https://en.wikipedia.org/wiki/Maximum_likelihood_estimation
the -2log(Likelihood) in your picture is a good hint that it's probably used.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How are Gamma-Poisson Distribution Fit Parameters Determined? They differ from a least-squares
normaly with MLE (maximum likelihood estimation)
https://en.wikipedia.org/wiki/Maximum_likelihood_estimation
the -2log(Likelihood) in your picture is a good hint that it's probably used.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How are Gamma-Poisson Distribution Fit Parameters Determined? They differ from a least-squares
I figured this out shortly after posting the question but then couldn't edit the question as the site was down. :(
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us