- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Generating conditional and marginal R-squared for mixed models
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Generating conditional and marginal R-squared for mixed models
I am running a series of mixed models in JMP 16 (one random effect, multiple fixed effects).
I would like to generate estimates of:
- Marginal R^2 (R^2m): the proportion of variance explained by the fixed effects relative to the overall variance
- Conditional R^2 (R^2c): the proportion of variance explained by both fixed and random effects relative to the overall variance
Is there a script readily available?
In addition, how does JMP compute the R^2 and adjusted R^2 in the "Summary of Fit" tab in the Fit Model report for a mixed model?
Note regarding conditional and marginal R^2: The method proposed by Nakagawa & Schielzeth (2013) applies to random intercept models. Johnson (2014) proposed an extension for models that include random slopes (see also Nakagawa, Schielzeth, & Johnson 2017).
Johnson, P. C. D. 2014. Extension of Nakagawa & Schielzeth’s R2GLMM to random slopes models. Methods in Ecology and Evolution 5: 944–46. doi:10.1111/2041-210X.12225.
Nakagawa, S., & H. Schielzeth. 2013. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods in Ecology and Evolution 4(2): 133–42. doi:10.1111/j.2041-210x.2012.00261.x.
Nakagawa, S., H. Schielzeth, & P. C. D. Johnson. 2017. The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. Journal of the Royal Society Interface 14(134). doi:10.1098/rsif.2017.0213.
- Tags:
- windows
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
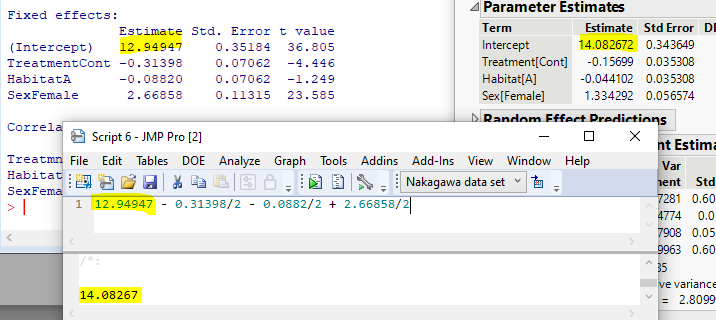
This screenshot show how intercepts are matched under different encoding schemes. And yes, those extra terms are not clear to me. In addition, the authors mentioned not to use degree of freedom correction for computing variances. All those are important details but not clear to me.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
Sorry, one more related question. If one was going to approximate the conditional R^2 from the full model output in JMP, would you suggest using R^2 or adjusted R^2?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
"Sorry, one more related question. If one was going to approximate the conditional R^2 from the full model output in JMP, would you suggest using R^2 or adjusted R^2?"
Do you mean whether use JMP's R^2 or JMP's Adjusted R^2 to approximate the conditional R^2 in the paper? If so, I am not sure. Is there an "adjusted" version for the conditional R^2?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
Yes, I meant whether to use JMP's R^2 or JMP's adjusted R^2 (both deviate slightly from the conditional R^2 in the example)
I have not seen reference to an "adjusted" conditional R^2 in the literature.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
Additional observation: the intercept value from JMP also differed from that reported in the paper for the full model, but the intercept was the same as that reported for the null model. Another small difference in the results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
"Additional observation: the intercept value from JMP also differed from that reported in the paper for the full model, but the intercept was the same as that reported for the null model. Another small difference in the results. "
That is expected. The encoding in JMP will make the intercept the ground mean in this case. How to match the intercepts under the full model, see my earlier post.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
Opinions, suggestions, tentative conclusions...
- Proposed conditional and marginal R^2 are conceptually similar to what JMP's traditional R^2 wants to summarize. JMP's traditional R^2 does not have any of the problems the authors want to address in the early part of their paper.
- The calculation of proposed conditional and marginal R^2 is not clear to me. Using the information available from model fitting, I cannot reproduce their results. There is important information not clear to me.
- If you can reproduce their results, then you may use them.
- If you cannot reproduce their results, don't say JMP's traditional R^2 are approximations to theirs. That is unknown. Doubts:
- If JMP's traditional R^2 is always close to theirs, why prefer a complex calculation to a simple calculation.
- If JMP's traditional R^2 and their versions are different from time to time, then a better understanding is needed, starting with reproducing their results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
I agree with your concerns. However, the literature does suggest that an R^2 generated from a mixed model is inherently problematic. That said, some measure of the variation explained by the model terms is useful (and quite different from using AIC to select among candidate models).
My understanding is that R^2 and adj. R^2 produced by JMP are intended to represent the variation explained by the combination of random and fixed effects, i.e., the model in total (akin to the conditional R^2).
How would you describe the R^2 obtained by regressing raw against the predicted values, as you suggested earlier?
Thanks for the continued discussion on this topic.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
The R^2 calculated using predicted values is the counterpart of the marginal R^2 in the paper. JMP does not produce that version of R^2. I cannot think of why I should use it in the context of mixed models.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
If one is forced to use a mixed model due to the presence of a random effect (e.g., a whole plot in split-plot experimental design), but one is primarily interested in the fixed effects (experimental treatments), the "marginal" R^2 would provide a measure of the variation explained by the fixed effects.
Thanks for your feedback.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us