- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Full Factorial + Center Points
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Full Factorial + Center Points
Dear JMP Community,
I am testing the full factorial with center points. Below are the input:
- Factors = 3 , Levels = 2 (Continuous data).
- Response = 1 (Continuouse data).
- Center Points = 6
- Replicates = 4
- Simulated Response using Normal Density Function with Sigma=1.
I have two questions:
1. Can this design detect curvature effect?
2. If yes, can it tell us which quadratic factor is responsible and estimate it's coefficient?
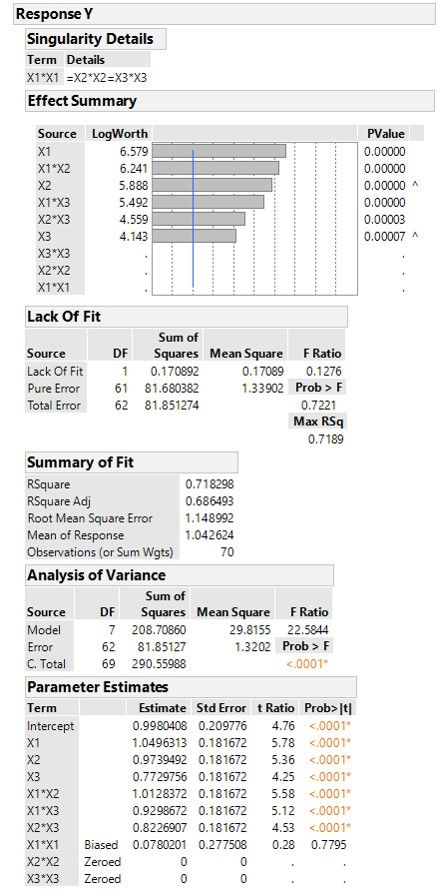
The reason I asked is because, it seems the answer is "no" to those two questions. Refer to below resutls.
In this case, what is the purpose of having the option of adding center point in Full Factorial, besides better to estimate the experimental error?
Thanks for the pointer.
B.r,
Looi
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Full Factorial + Center Points
Your lack of fit p-value is what you use to detect curvature, but you cannot determine the source if you have > 1 continuous factors. You cannot actually model any quadratic effects with this design. The 2-level factorial designs will only allow you to fit a hyperplane surface to the data. If the center points are significantly biased as a group away from the hyperplane, your lack of fit test will have a small p-value.
As @Peter_Bartell alluded to, you have a huge run budget. Using center points in a factorial design (full or fractional) is typical of screening scenario where you have too many factors to directly try to estimate a response surface, but you want to know if curvature is present. That is not your situation. You could do a decent response surface design for 3 factors with as few as 20 runs.
I would suggest following Peter's recommendation of an I-optimal design using Custom Design and specifying your model with the RSM button. That will give you all main effects, 2-factor interaction, and quadratic terms. If you can accomodate off-face axial values, a central composite design (CCD) has significant advantages over the I-optimal Custom Design for the same number of runs. You will get much higher power for your quadratic effects in most cases. If you're set on 60+ runs, you could even replicate the full CCD a couple times. If you're unfamiliar with optimal designs, creating a CCD is probably more straight-forward as well. Just make sure you are confident the axial values have set points you can actually run.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Full Factorial + Center Points
The sort of old fashioned idea behind adding center point replicates was two fold: 1. Detect curvature in at least ONE of the factors, and 2. Provide some extra degrees of freedom for LOF tests, Pure Error and their brethren. Why one would add center point replicates to an already replicated design to me seems to negate 2. above. The only other reason would be to detect curvature. But I guess I would ask, if you have a budget for 60+ runs, why not just run a full blown i - optimal design in your factors, and if you need some pure error, add a small number replicates in that design. Then you could estimate curvature rather than just detect it. At far fewer runs.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Full Factorial + Center Points
Your lack of fit p-value is what you use to detect curvature, but you cannot determine the source if you have > 1 continuous factors. You cannot actually model any quadratic effects with this design. The 2-level factorial designs will only allow you to fit a hyperplane surface to the data. If the center points are significantly biased as a group away from the hyperplane, your lack of fit test will have a small p-value.
As @Peter_Bartell alluded to, you have a huge run budget. Using center points in a factorial design (full or fractional) is typical of screening scenario where you have too many factors to directly try to estimate a response surface, but you want to know if curvature is present. That is not your situation. You could do a decent response surface design for 3 factors with as few as 20 runs.
I would suggest following Peter's recommendation of an I-optimal design using Custom Design and specifying your model with the RSM button. That will give you all main effects, 2-factor interaction, and quadratic terms. If you can accomodate off-face axial values, a central composite design (CCD) has significant advantages over the I-optimal Custom Design for the same number of runs. You will get much higher power for your quadratic effects in most cases. If you're set on 60+ runs, you could even replicate the full CCD a couple times. If you're unfamiliar with optimal designs, creating a CCD is probably more straight-forward as well. Just make sure you are confident the axial values have set points you can actually run.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Full Factorial + Center Points
Appreciate both the inputs. This is the first time I post a question, and I am amazed on how fast the reply came in. Definitely increases my confidence to keep using SAS JMP.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us