- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: DoE analysis : Removing non significant main factors when they are implicate...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
DoE analysis : Removing non significant main factors when they are implicated in a significant interaction
Hey Jmp users,
Is it possible to remove non significant main factors when they are implicated in a significant interaction in DoE data analysis ?
Thanks !
I
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE analysis : Removing non significant main factors when they are implicated in a significant interaction
Hi,
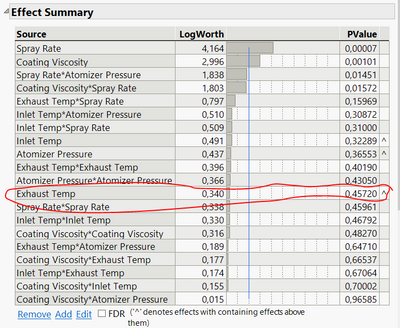
Yes, it is possible. When analyzing a DOE using Fit Model, the lower-order effects that are contained within higher-order effects are denoted with a circumflex symbol (see image below). You will get a warning message if you try to remove it, with the option to "remove only non-contained effects," but you have the option to ignore this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE analysis : Removing non significant main factors when they are implicated in a significant interaction
Hi,
Thanks for your answer. I wanted also to ask from a statistical point of view, does it affect your model ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE analysis : Removing non significant main factors when they are implicated in a significant interaction
Hi,
The principle is called "effect heredity." There is a brief mention of it in the "Principles and Guidelines for Experimental Design" (https://www.jmp.com/support/help/en/15.2/index.shtml#page/jmp/effect-heredity.shtml). Basically, if a main effect isn't significant than the higher-order term likely isn't significant either.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE analysis : Removing non significant main factors when they are implicated in a significant interaction
Actually the principle is Effect HIERARCHY. That is if higher order terms are significant, then the lower order terms should be included in the model. (Heredity principle is the for a higher order term to be active at least one of the lower order terms (parents) must be active).
To be clear, what you really need to do is understand the interaction. Since an interaction is when the effect of a factor depends on another factor, you need to understand this effect. For 2-level designs, there are 4 possible factor combinations for 2nd order effects: -1,-1, -1,1, 1,-1, 1,1. A significant interaction means there is a difference in effect between when the factors are at the same level vs. when they are at opposite levels.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE analysis : Removing non significant main factors when they are implicated in a significant interaction
I thought the principle was "hierarchy," but it seemed to be described differently in the documentation: it seems to say that Hierarchy relates to higher-order terms generally not accounting for as much variation as lower-order terms, and Heredity "relates to the inclusion in the model of lower-order components of higher-order effects."
Effect Hierarchy: https://www.jmp.com/support/help/en/15.2/index.shtml#page/jmp/effect-hierarchy.shtml#
Effect Heredity: https://www.jmp.com/support/help/en/15.2/index.shtml#page/jmp/effect-heredity.shtml#
It could be that I'm confusing the principles or that I misinterpret the documentation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE analysis : Removing non significant main factors when they are implicated in a significant interaction
The confusion arises because the same word ('hierarchy') is used in two different contexts to describe different things. The 'hierarchy principle' is assumed by screening designs. It says that the effects of factors tends to decrease as the order increases. So third-order effects tend to be smaller than second-order effects and can be ignored. 'Model hierarchy' is a statement about the structure of the linear predictor. It says that a hierarchy of terms exists when one term is present in another term. So a linear predictor such as β0 + β1*X1 + β2*X2 does not exhibit model hierarchy but another linear predictor such as β0 + β1*X1 + β2*X2 + β12*X1*X2 does exhibit model hierarchy.
(The 'heredity principle' that is also assumed by screening designs says that active higher order terms tend to involve factors that exhibit active main effects.)
Model hierarchy is important. I wrote an article about it for the JMPer Cable newsletter years ago. In the second case above, it is not illegal to remove the β1*X1 term or the β2*X2 term, but it is not advised. Hence, JMP allows this action but warns you not to do it. Why maintain the model hierarchy? Because if you change the scale of your factors, you necessarily change the structure of the model. Some terms will disappear. New terms will appear. People do not like surprises.
But you never change the factor scale! Well, you might. The regression analysis of a DOE is based on centered and scaled factor levels known as 'coded levels.' So the parameter estimates are based on a predictor scale from -1 to +1. You can back-transform or un-code the factor levels so that the parameter estimates are in terms of the real scale. Not an unreasonable desire. Well, you will necessarily change the structure of the model from what you selected to something else.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us