- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: DoE How to treat replicate measurements
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
DoE How to treat replicate measurements
(I needed to extend the question, the update is below the images)
Hey everyone,
I am looking for some advice. I have performed a definitive screening design (JMP 11) with 3 factors, 1 response (9 experiments) three times. I augmented the design and entered the new data. The problem is, that some combinations produce very varying results. I have repeated some of these experiments additional three times and the variation seems to be "inherent".
My question is how to treat these replicate runs. When I augment the design to have 2 replicate runs (3 runs in total), my regression looks pretty bad.
However, when I average my trial runs first and then perform the regression, I get much better results.
But when I do the averaging first, I think I disregard the information about the standard deviation/variance, which I would like to include (and maybe penalize, because we would like to work in a "stable" region).
Is there any way to include this into the DoE? Maybe use the SD as a response and minimize it?
Edit:
I've thought about my problem and would like to extend it a "little" bit. I thought that I could use the SD as weight for my data, in order to take into account that some conditions used for the experiments lead to very varying results and others are more reproducable. So I read about weighted least square regression and now I am very confused because choosing the weight appears to be non-trivial. Thus my question extends to: If I use a weight, which one would be appropriate. Currently I have thought about and tried the following approaches:
- Use the SD (from what I have seen, it should used as 1/SD or 1/SD^2). This sounds very reasonable to me but on the other hand I have read that one needs lots of replicates to have a proper estimate of the SD (in the range of dozens), otherwise this method is not accurate enough.
- Use one of my responses as a weight. I am also measuring the so called polydispersity index, which gives me some information about the homogenity/heterogenity of my samples. The results looks quite good, but I am not sure if it is allowed to use a response a weight (I think I would introduce some kind of bias?)
- Use the residuals. I have found this in a lecture handout. The idea is to make a non-weighted fit first and the use 1/(residuals)^2 as the weight. But againg, I am worried to "push" the resulting fit into a wrong direction.
Thanks a lot!
Nachricht geändert durch Roland Goers
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE How to treat replicate measurements
After you create your RSM with your design variables, add the Rep variable. At this point it is considered a Fixed effect, and will appear in the model equation. Go ahead and do the regression this way first. You can check to see if it is significant, and how big an effect it is. If it is significant, transform the Rep variable to a 'Random Effect' (click the Attributes red triangle), and do the regression again. This time it will not appear in the model equation, rather, it is considered a random effect. "A random effect is a factor whose levels are considered a random sample from some population. Often,...variance components). However, there are also situations where you want to predict the response for a given level of the random effect. Technically, a random effect is considered to have a normal distribution with mean zero and nonzero variance."
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE How to treat replicate measurements
Roland,
I can think of a few things I would do if I were in your situation.
First, if you feel the replicates are showing excessive variation, perhaps you have missed one or more key input variables that are varying without your knowledge. Also, what about your measurement system? Is you measurement stable?
You might also "normalize" your input variables before analysis (like calculating a Z score) - Subtract each value in the input column from the average of that column and divide the difference by the standard deviation of that column. Now you have a new column of normalized values.
Even though the amount of data is small, I sometimes go ahead and try some predictive modeling like partition and neural networks. Sometimes you get some good clues here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE How to treat replicate measurements
Thank you very much for your answer!
I think the experimental setup is fine, even though I agree that there are probably more factors which should be taken into account. However, these are factors we do not know (yet) and/or cannot control. That's one of the issues in fundamental research
I followed you advise and read and computed the z-score for my measurements. I used them as weights during the regression and the results look promising. Close to the regression I obtained when I simply used the mean values, which I think makes sense.
However, I've read that similar to the 1/SD approach, it is required to know the population mean and its SD. But as the experiments are very time consuming, I think this might be a trade-off I need to "risk".
Of course, if anyone knows a better way for data with small numbers of replicate runs, I would be happy to try it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE How to treat replicate measurements
Roland, in general there are three sources of variation: the process, sampling, and the measurement system. From what you describe, it sounds like you have significant variation in sampling and/or measurement. Consider a Components of Variance (nested, hierarchical) designed experiment to isolate the sources of variation and their contribution to the overall experimental variation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE How to treat replicate measurements
{continuing...} I have many times in research found the sampling and/or measurement variation to be so great as to obscure the effects of the controllable factors we were investigating. Sometimes just a thorough review of how the experiment is run, samples taken, and measurements made revealed differences (among those involved in the "system" for example) that were causing the large variation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE How to treat replicate measurements
Do you mean Mixed and Random Effect Model Reports and Options ? I will read about it and see how I can implement this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE How to treat replicate measurements
The Components of Variance design would be represented by a Random Effects model. You can read about them in this excerpt from Box, Hunter, Hunter's _Statistics for Experimenters_": https://app.box.com/files/1/f/74723508/1/f_9510142201.
The excerpt also includes a detailed explanation and example of how to optimize (e.g., minimize cost) the sampling and measurement for a desired total experimental variance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE How to treat replicate measurements
I want to be clear about your protocol. You actually replicated runs, not merely measured the outcome more than one. For example, the response in an experiment to study the make up of a chemical buffer might by the pH. My treatments define different levels of ingredients in each buffer. Each run produces a new buffer solution. If I make another solution, that is replication and observing the resulting pH provides new information. If I simply measure the pH of the same buffer solution three times, that is a repeated measurement.
If you actually replicated runs then you should include all the individual replicates in the analysis and not the average. The root mean square error estimates the random variation between runs. The mean square error provides the proper denominator in the ANOVA F-test and the root mean square error provides the proper standard error for the parameter estimate t-tests.
On the other hand, if you simply repeated the measure of the response for a single run, then using the average makes sense ifyou believe that the variation in the repetitions is purely in the measurement (repeatability).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE How to treat replicate measurements
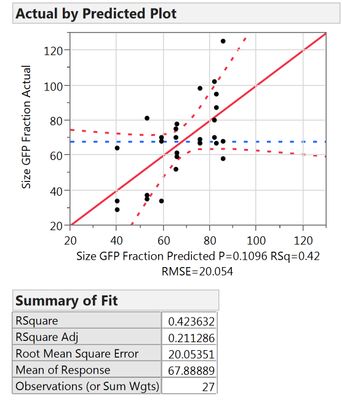
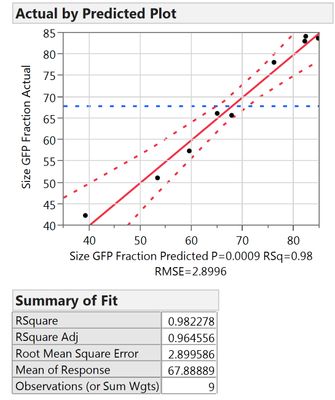
All samples I measure are prepared individually, thus I think I did "true" replicates. They are also all included in the analysis (the design consists of 9 runs, I entered 27 data points). The result is shown in figure 1.
Maybe it helps if I briefly descirbe what I am doing or want to do: I try to produce some kind of protein decorated nanoparticles for my PhD thesis. The creation relies totally on the self-assembly of the components, thus I can control the composition and the evironment (e.g. temperature in the lab) but the formation takes place over 2 days and is spontaneous.
We do not really understand what happens during that time, we only have a rough idea of what should happen. My idea was to use DoE to get a better idea what the important factors are and how they influence the outcome. The factors I have chosen to investigate are the most likely ones, determined from former experiments. In the end, this experiment should tell me, which parameters I have to adjust in order to obtain particles of a certain size and as homogenous as possible.
In these experiments, there seem to be parameters which give varying results (I did another triplicate for this compositions). Other conditions appear to be much more reliable. Thus I would like to able to make a statement like "On average we get this size, however this parameter region is "unstable", this one here is more "stable"". And of course, the model would need to reflect this. That's why thought about including the SD as a weight and use the PdI as a second response (max. size, min. PdI).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE How to treat replicate measurements
re: "Do you mean Mixed and Random Effect "
Actually, I mean Fixed and Random effects.... Yes, do check out these tools.
After you add a 'Rep' or 'batch' variable to your data, make sure it is nominal categorical type, then include this an an input factor in your model regression, along with your design factors. Why you are at it, were there any other uncontrolled variables that you tracked, e.g. temperature variation, time, etc. ? If so, include those as well. By default the 'batch' variable will be a Fixed effect. This means it will appear in the model equation. This is useful to diagnose the magnitude of batch-to-batch effects and help to see where it occurs. As a main-effect, it will show only the offset for that particular batch.
If you specify the batch variable as a Random effect, it will not appear in the model equation. There are advantages to doing this, but is less useful at this point since you want to 'see' the variation effects.
When you include all individual reps (as opposed to the means) you are able to get Lack Of Fit diagnostics, which are very useful to help understand the process, to highlight any lurking effects. I recommend always regressing the individual reps, although I understand it is sometimes useful to use the means as a second step.
I like your idea of including the size variation as a second response. Although, I would not recommend using any weighting schemes at this point.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us