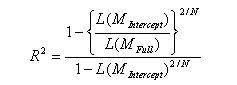- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Difference in results between Generalized RSquare and RSquare
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Difference in results between Generalized RSquare and RSquare
Hi everyone,
I tried to find an answer to my question in the community or in JMP help, but I couldn't. So, I would really appreciate if anyone could point me in the right direction here or let me know what is the basic concept I am missing.
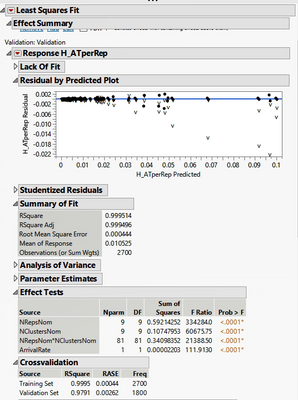
I am fitting a model to my response (dependent variable - DV), which is continuous, using 3 independent variables (IV) [2 categorical and 1 continuous] and the interaction between 2 of them (the other one I am just using the main effect). I first used Least Squares for that, as you can see in the screenshot below.
However, my residual by predicted plot does not look very good (I have some outliers). No matter which other factors I tried to add to the model - or transformation - I was not able to improve my residuals plot. The best I could get was using a change of my response, which is the one I am already showing above.
Next, I thought about using the Penalized Regression Method (more specifically Ridge) through the Generalized Regression. I read it can be more robust to outliers (though it will introduce some bias).
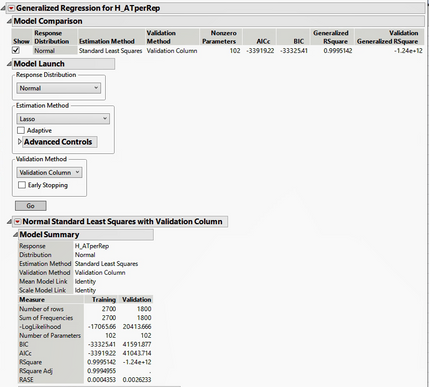
I started running the Generalized Regression with Standard Least Squares.
According to some videos I have seen, this should produce the same results as the Least Square regression.
Also, according to JMP help (https://www.jmp.com/support/help/en/15.2/index.shtml#page/jmp/training-and-validation-measures-of-fi...) the Generalized RSquare provided should be between 0 and 1 and it will simplify to the traditional RSquare for continuous normal responses in the standard least-squares setting. However, as you can see from the screenshot below, although the Generalized RSquare matches the RSquare for the Training set, it does not match for the Validation set (and it is negative). The other statistics (e.g. RASE) do match both sets (Training and Validation).
Any ideas about what may be happening here?
Thank you in advance for any ideas and hints!
PS: For everything I am doing in this post, I used the FitModel platform in JMP.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference in results between Generalized RSquare and RSquare
Is the continuous predictor involved in the interaction term? Did you use the estimate for the omitted interaction to determine that it should be removed or did you leave it out to begin with?
What transformations of the response did you try?
Penalized regression and least squares regression do not usually lead to the same estimates of the model parameters, so the R square would not be the same. Your picture shows the OLS result, not the Ridge Regression.
The training and validation results should be similar with the best unbiased model, but not the same. How did you determine the hold out set for validation?
The negative R square is possible.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference in results between Generalized RSquare and RSquare
Sorry @Mark_Bailey, I think I was not very clear in my question.
As you stated I did not use Ridge (that was gonna be my next step). But first, I just used again the Least Squares method (through the Generalized Regression model), to check if the results would match with the results using LeastSquares directly from the FitModel window. Because my results did not match, I did not even end up trying Ridge (which would be my next step).
But I am curious why the results from LeastSquares through Generalized Regression are not matching the results through LeastSquares directly from FitModel. Do you have any ideas?
Answering your questions:
1. The continuous predictor is not involved in the interaction term.
2. I used stepwise and also used the estimates myself to determine whether the interaction effect should be removed
3. I tried Log, Logistic, Logit, and Reciprocal. With reciprocal, the model deteriorates a lot. With Logistic, there is a slight improvement in the statistics (R-square, RASE), but not in the residual plots. So nothing to justify the use of the transformation in my opinion.
4. The training and validation were defined based on groups I have (these are computer experiments with different random seeds). I used the seeds to separate the data in groups and used that column as my holdout validation column.
5. My question related to negative was for Generalized R-square, cause when I first read the JMP help, I thought it could only go between 0 and 1. But yes, I found the formula for that one and as we can see it can also go below 0:
| Nagelkerke / Cragg & Uhler’s (Generalized RSquare) |
Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference in results between Generalized RSquare and RSquare
I noticed in your original residual plot that the outliers all seem to be in the validation hold-out set.
Generalized Regression uses a different parameterization than Fit Least Squares. See this page of statistical details. It also uses a different estimation method (MLE vs OLS).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference in results between Generalized RSquare and RSquare
Hi @Mark_Bailey , thank you so much for getting back to me again. I really appreciate all your help and patience with my questions.
Yes, for this specific response all my outliers are in the validation set. But for other responses I am investigating, this is not true (the outliers fall in both the validation and training sets).
In terms of what I am modeling: I had run a few experiments using discrete event simulation (with different seeds so that I would have different data). Based on that I calculated my four responses of interest (here I showed only one).
Now, I am trying to fit a regression model to those responses, because my next step will be to use an optimization model to find the best setting for my responses of interest.
As far as I know, the parameterization/coding should not impact the model statistics. Am I missing something here? (Coding)
Also, for linear regression and when residuals are normally distributed, OLS and MLE lead to the same coefficients. Don't they? (OLS and MLE)
According to this Generalized Regression tutorial posted by @gail_massari , around time 8:35, my understanding is that @brady_brady also says that the results between the MLE and the OLS should match.
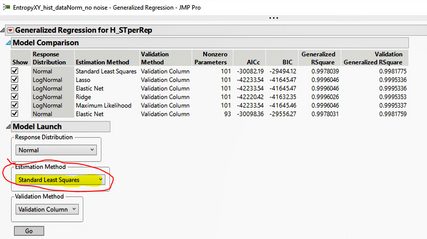
Finally, would you mind pointing me to the JMP help page that indicates the Generalized Regression uses MLE instead of OLS when the distribution is normal?
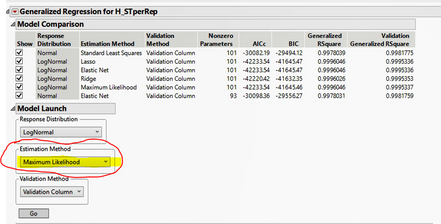
Because of the image below (taken from JMP), I was under the wrong impression that the Generalized Regression would still use OLS if the distribution chosen was Normal:
Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference in results between Generalized RSquare and RSquare
You are correct, the metrics for the whole model should not change with different parameterizations. Of course, the metrics for individual terms or parameters will change.
So the coefficients are not the same with different parameterizations, so their estimates must be different, too.
The OLS solution and the MLE optimization should lead to the same estimates under the same parameterization with a normally distributed response.
I misled you: the standard least squares result in GenReg is OLS. See this page for more details.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference in results between Generalized RSquare and RSquare
Thank you for all the details and for pointing me to more information about the GenReg.
But I am still confused in this case (assuming normal distribution for the response), what would explain the differences in the Generalized Rsquare values between the validation sets among the two "platforms" (Fit Least Squares and GenReg)?
Sorry if I misunderstood something you said.
Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference in results between Generalized RSquare and RSquare
I cannot say from this discussion what might cause a difference. I suggest that you contact JMP Technical Support (support@jmp.com) about the matter.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference in results between Generalized RSquare and RSquare
I will post the answer here when I have it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference in results between Generalized RSquare and RSquare
Hi @AnnaPaula ,
If I understand correctly, you have a data set that you have split according to a validation column of some kind. One thing to consider is whether or not you stratified the validation column on your response to make sure both the training and validation columns have similar distributions.
Since the R^2 is negative, to me that would indicate you're overfitting your data. Have you done some bootstrapping on the estimates to see if the terms you have in your model are really important? Do you have a theoretical basis for including mixed terms?
Also, you might want to try Elastic Net since it's a combination of Ridge and Lasso. Another thing to consider is if your response distribution is really normal or if a different distribution is better suited to your data.
DS
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us