- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Difference between "least square" and "generelized linear method" in the fit mod...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Difference between "least square" and "generelized linear method" in the fit model
Hello Community,
There is something that I have not understood between the difference of the results I get when analyzing a small dataset by using fit model with “standard least squares” and then using the Box Cox transformation menu to do a log transformation (λ = 0) versus using the same “fit model” but this time with “generalized linear model” with distribution “Normal” and link function “log”.
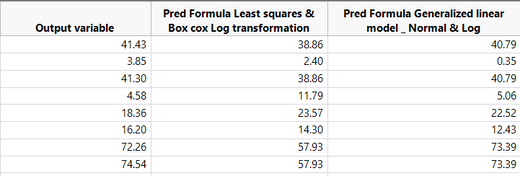
See the results in the table below. I preent the actual response values (clumn output variables), then a second colulmn with the prediction from the method least squares with the log transformation and finally a third column with the results using the method generalized linear model with normal distribution and log link function. You can clearly see that generalized linear model method does better predictions. I wonder why the least squares method with the log box cox transformation do not give as good results (or similar) as the ones by the generalize linear method with normal distribution and Log link function.
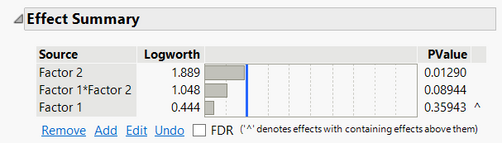
I specify that the terms of the model in both cases are the same (two main effects and one interaction). Knowing what the difference between these two methods is and if I can decide using one or the other without restrictions is crucial since if you se the results below the significance of terms are also different in each case. To be honest, the generalized linear method reflects more accurately the real situation we observe. However, I do not exactly know if I can use freely the generalized linear method. I looked in the documentation but found only general information about some nonnormal cases (binomial count etc) where generalized method can be used, but my question is a little bit more precised.
Effect summary for least squares method with Log box cox transformation (λ = 0)
Effect summary for Generalized linear method with normal distribution and log link function
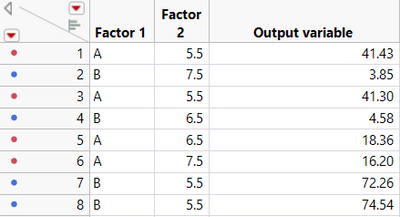
I provide here below the whole table I you wish to verify/test the method:
Thank you for reading and I can provide further information if needed.
- Tags:
- windows
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference between "least square" and "generelized linear method" in the fit model
Hi @Julianveda,
Welcome in the Community !
Transforming the response with log is indeed not the same as using a GLM with log link. It's like comparing the average of the log response, versus the log of the average response.
Applying a non-linear (e.g., log, inverse) transformation to the dependent variables not only normalizes the residuals, but also distorts the ratio scale properties of measured variables.
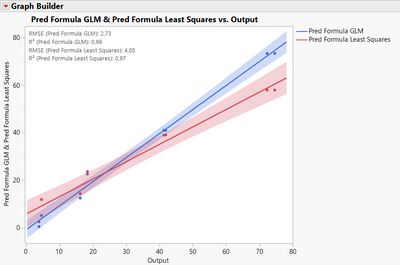
On your example, we can see that using log transformation with a standard least squares model tends to underperform for bigger Y values, as differences in big Y values lead to very small log differences (it "shrinks" the differences because of the log transformation).
Example with rows 1 and 7 (output difference is equal to 30,43), where the difference of the log of the individual responses is equal to 0,237 whereas the log of the difference between the row is 1,483.
Applying GLM and setting up this type of model with link function enable to stay in the original scale of the data, using a link function to transform the mean into a linear function of the predictor variables and a variance function to allow for variance heterogeneity in the analysis rather than trying to transform it away (for example through log transform).
I added the datatable and scripts used for the comparison, and if other experienced users want to use the dataset for further explanations.
Some references for further explanations/reading :
- https://stats.stackexchange.com/questions/47840/linear-model-with-log-transformed-response-vs-genera...
- http://faculty.washington.edu/heagerty/Courses/b571/homework/Lindsey-Jones-1998.pdf
- http://www.leg.ufpr.br/~joel/Rmodelling/Slides/transforms.pdf
- https://www.frontiersin.org/articles/10.3389/fpsyg.2015.01171/full
@Mark_Bailey you can use the dataset I attached, it shows some patterns in the actual vs. predicted and residuals :
I hope you'll better understand the difference between the two modeling techniques.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference between "least square" and "generelized linear method" in the fit model
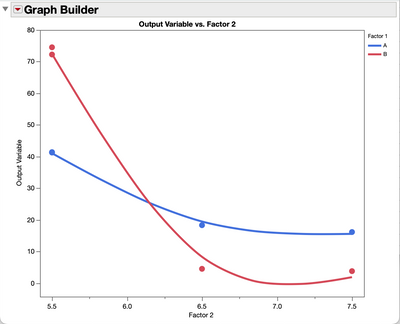
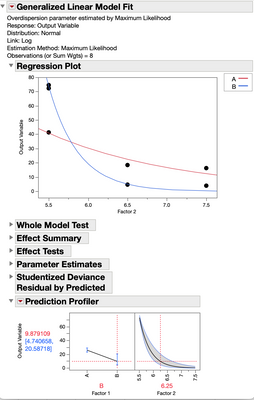
Graphing your data reveals the nature of the model you need to fit to this data. There is a quadratic effect of B that interacts with factor A:
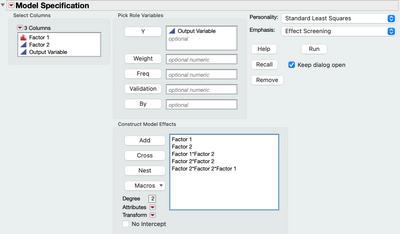
This means that the appropriate least squares model to fit to this data is:
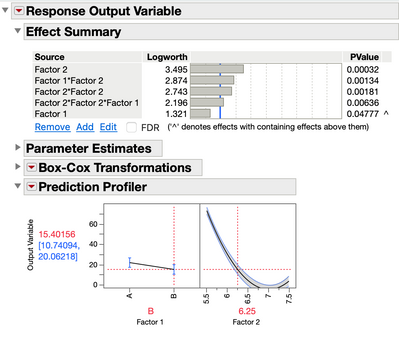
Which gives:
Note the dramatic change in the profiler regarding the effect of Factor 2 on the output variable when switching factor 1 to the B setting:
You will find this profiler looks very similar to that you are getting via your General Linear Model approach which is able to model the nonlinear relationship in your data.
The short answer is: your least squares model and general linear model are not equivalent with regard to their ability to model the curvature in this particular data. Graphing the data prior to specifying the model will help to work out the model to specify in standard Least Squares.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference between "least square" and "generelized linear method" in the fit model
Thank you @malcolm_moore1 for your reply. I forgot to mention that for us a cuadratic effect of factor 2 does not make physic sense. Therefore, we decided to only consider the two main effects and the interaction and look for the best possible model using these. It was under this condition that we found that least squares seem underperformed when compared to generalized linear model. However, I do not master yet enough the generalized linear model to propose it as a solution.
Concerning the graphic builder, I actually use it and thanks to that I realized the exponential fitting that was what led me to try logarithmic transformations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference between "least square" and "generelized linear method" in the fit model
Please look at the profiler for your generalized linear model. This shows your generalized linear model is representing the relationships in your data in the same way as the model I proposed by using standard least squares (representing the effect of Factor 2 as non-linear). If a non-linear effect makes no physical sense then you shouldn't be using the generalized linear model.
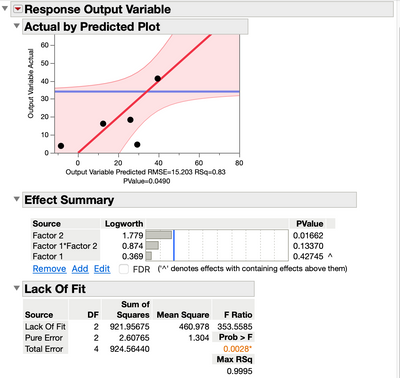
Please go back to the least squares model with linear and two factor interaction effects and turn on the option for lack of fit test. You will see evidence of lack of fit:
If the effect of factor X2 cannot be non-linear, then I encourage you to think about what is responsible for the lack of fit. For example is there another factor that was not controlled or measured in your experiment that might also be influencing your output? There is something going on in your process that is not explained by the linear effect of X1, the linear effect of X2, or the interaction effect of X1*X2. This lack of fit is responsible for the poor predictive quality of the least squares model for rows 2 and 4.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference between "least square" and "generelized linear method" in the fit model
Thank you @malcolm_moore1 for your answer and recommendations. It is not non-linearity that does not make physical sense in our situation, it is the cuadratic term or higher interaction terms. The GLM is not linear but precisely describes this situation using only terms that for us also mean something from a mechanistic point of view.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference between "least square" and "generelized linear method" in the fit model
This is great justification for using the GLM model if it better represents your expectations based on scientific knowledge. If there are other mechanistic relationships you wish to represent in the future then you might also wish to explore Fit Curve or Non-linear.
Otherwise it is helpful to bear in mind that many statistical methods are empirical by nature - they give a model that approximates the trends in your data but do not aim to describe the underlying mechanisms. A statistical/empirical model may be sufficient to achieve a goal within the range of the data collected, e.g. suggest settings of the X variables that achieve desired outcomes of the Y variables associated with an improvement or optimisation goal based on experimentation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference between "least square" and "generelized linear method" in the fit model
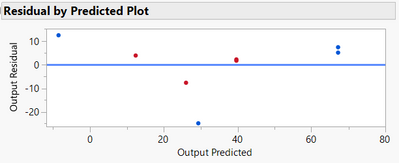
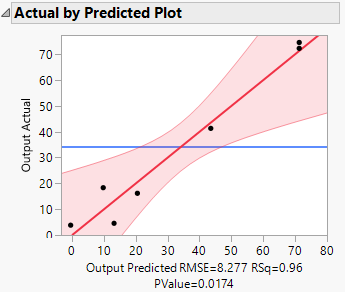
What led you to apply a transform to the output? The Actual by Predicted plot does not exhibit a pattern:
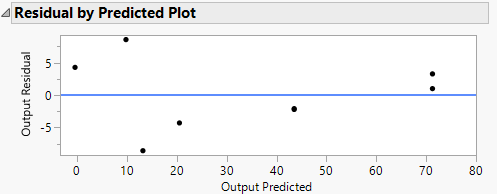
Neither does the Residual by Predicted plot:
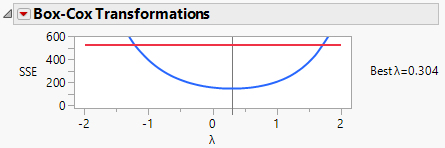
The wide 95% confidence interval on Lambda in the transform function includes 1, the identity transform:
You have a small data set with which to evaluate transforms.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference between "least square" and "generelized linear method" in the fit model
Thank you @Mark_Bailey for your answer. What led me to look for a finer solution was the fact that the analysis by "least squares" did not show a significance for factor 1, but we were in reality observing it. Also, as explain in my reply above, plotting in the graphing builder we observed exponential behavior.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference between "least square" and "generelized linear method" in the fit model
Lack of fit can also mask effects. You did not expect a quadratic effect, but the limited data suggests curvature, nevertheless.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference between "least square" and "generelized linear method" in the fit model
Thank you @Mark_Bailey for your answer. It is not curvature or non linearity that does not make physical sense in our situation, it is the cuadratic term or higher interaction terms. The GLM is not linear but precisely describes this situation using other mathematical functions (differnt from quadratic or high order polynomials) and using only terms that for us also mean something from a mechanistic point of view.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us