- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Difference between "least square" and "generelized linear method" in the fit mod...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Difference between "least square" and "generelized linear method" in the fit model
Hello Community,
There is something that I have not understood between the difference of the results I get when analyzing a small dataset by using fit model with “standard least squares” and then using the Box Cox transformation menu to do a log transformation (λ = 0) versus using the same “fit model” but this time with “generalized linear model” with distribution “Normal” and link function “log”.
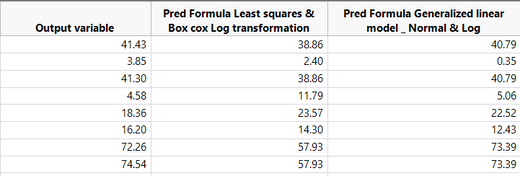
See the results in the table below. I preent the actual response values (clumn output variables), then a second colulmn with the prediction from the method least squares with the log transformation and finally a third column with the results using the method generalized linear model with normal distribution and log link function. You can clearly see that generalized linear model method does better predictions. I wonder why the least squares method with the log box cox transformation do not give as good results (or similar) as the ones by the generalize linear method with normal distribution and Log link function.
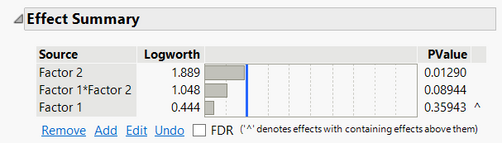
I specify that the terms of the model in both cases are the same (two main effects and one interaction). Knowing what the difference between these two methods is and if I can decide using one or the other without restrictions is crucial since if you se the results below the significance of terms are also different in each case. To be honest, the generalized linear method reflects more accurately the real situation we observe. However, I do not exactly know if I can use freely the generalized linear method. I looked in the documentation but found only general information about some nonnormal cases (binomial count etc) where generalized method can be used, but my question is a little bit more precised.
Effect summary for least squares method with Log box cox transformation (λ = 0)
Effect summary for Generalized linear method with normal distribution and log link function
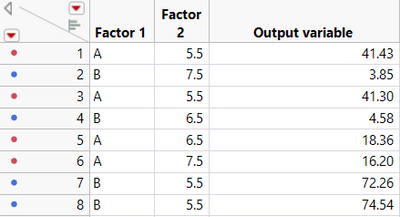
I provide here below the whole table I you wish to verify/test the method:
Thank you for reading and I can provide further information if needed.
- Tags:
- windows
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference between "least square" and "generelized linear method" in the fit model
Hi @Julianveda,
Welcome in the Community !
Transforming the response with log is indeed not the same as using a GLM with log link. It's like comparing the average of the log response, versus the log of the average response.
Applying a non-linear (e.g., log, inverse) transformation to the dependent variables not only normalizes the residuals, but also distorts the ratio scale properties of measured variables.
On your example, we can see that using log transformation with a standard least squares model tends to underperform for bigger Y values, as differences in big Y values lead to very small log differences (it "shrinks" the differences because of the log transformation).
Example with rows 1 and 7 (output difference is equal to 30,43), where the difference of the log of the individual responses is equal to 0,237 whereas the log of the difference between the row is 1,483.
Applying GLM and setting up this type of model with link function enable to stay in the original scale of the data, using a link function to transform the mean into a linear function of the predictor variables and a variance function to allow for variance heterogeneity in the analysis rather than trying to transform it away (for example through log transform).
I added the datatable and scripts used for the comparison, and if other experienced users want to use the dataset for further explanations.
Some references for further explanations/reading :
- https://stats.stackexchange.com/questions/47840/linear-model-with-log-transformed-response-vs-genera...
- http://faculty.washington.edu/heagerty/Courses/b571/homework/Lindsey-Jones-1998.pdf
- http://www.leg.ufpr.br/~joel/Rmodelling/Slides/transforms.pdf
- https://www.frontiersin.org/articles/10.3389/fpsyg.2015.01171/full
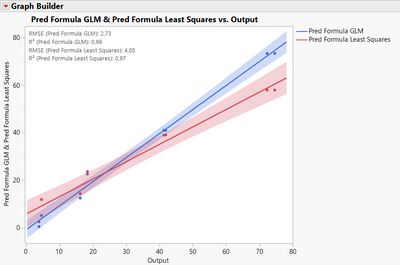
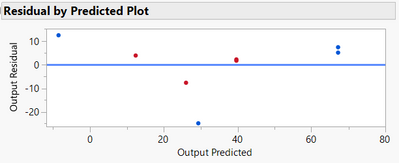
@Mark_Bailey you can use the dataset I attached, it shows some patterns in the actual vs. predicted and residuals :
I hope you'll better understand the difference between the two modeling techniques.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Difference between "least square" and "generelized linear method" in the fit model
Thank you @Victor_G for this very interesting and insightful information.
To be honest I do not understand everything in the provided links, but if I understood well the use of GLM can be justified in my case.
Please correct me if I'm wrong.
Julian
- « Previous
-
- 1
- 2
- Next »
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us