- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Definitive screening designs - correlated vs. confounded second-order effect...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Definitive screening designs - correlated vs. confounded second-order effects
One line I've seen mentioned regarding DSDs is that for any 6-factor experiment, the full response surface can be fitted within 3 factors. However, one of the tradeoffs of DSDs is that two-factor interactions are correlated with other two-factor interactions and quadratic terms, despite none of them being confounded. If I'm understanding this correctly, this at least allows us to estimate the two-factor interactions and quadratic terms independently as they aren't 'tied to' any other second-order terms. However, because of this partial correlation, the actual coefficient that is assigned to the second-order terms may be inaccurate.
My question then is: does it make sense to use the DSD for optimization purposes, even if you are able to fit the full RSM? It seems suboptimal that you would get a an estimate for the effect of a quadratic or interaction term, which is actually being influenced by other terms.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Definitive screening designs - correlated vs. confounded second-order effects
Good question, @QW !
Our estimate of an effect is always inaccurate when learning from a real-world stochastic process. "All models are wrong...". Our objective is a useful model, that is accurate enough that we can answer our scientific/engineering questions.
The correlation between higher order effects in a DSD will affect the precision of their estimation. You are literally correct in saying that a DSD is not optimal for estimating those effects.
Your alternative would be an optimal design that is specifically designed to estimate those effects. However, to improve the estimation of all second order effects for all factors will require more runs. The question then is whether the gain in precision is worth the extra effort of a larger experiment.
You don't get something for nothing and DSDs are remarkably efficient.
You should also consider that DSDs are screening designs, not final designs. They are primarily for screening for the important factors. You would then augment optimally if you need to improve precision of estimation of the effects of the "active" factors.
I hope all this helps,
Phil
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Definitive screening designs - correlated vs. confounded second-order effects
Hi @QW,
The answer from @Phil_Kay is excellent.
Just to clarify the topic of correlations (called "aliases") in the DSD : in DSD, there are no aliases (correlations) between main effects, and between main effects and interactions (or quadratic effects), so main effects can be estimated precisely and in an unbiased way.
But as you mention, there are aliases between interactions, and between interactions and quadratic effects. Since there are no complete correlations (confounding), the effects can still be detected and parameters can be estimated, but at the price of an higher standard error, so the parameters estimation will be less precise than if you have no aliases at all between effects.
Let's just remind that the "S" in DSD is for screening, so it's a very efficient design to screen main significant effects from a large number of continuous (and few 2-levels categorical) factors, but if you want to estimate precisely some terms to have a Response Surface Model, you may need to augment the design to gain more precision in estimating quadratic effects and 2-factors interactions. Or if you already have knowledge about your factors and/or a low number of factors, an Optimal design may be more suitable in estimating these effects.
So for optimization purposes, you may have the choice to augment a previous design like a DSD, or directly create a more customized model to suit your needs.
I hope this will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Definitive screening designs - correlated vs. confounded second-order effects
Just a slight correction to Victor's post. There is no aliasing between Main effects and 2nd order effects (interactions and quadratic). Higher order effects are indeed aliased. Whether this impacts precision or bias is conjecture.
One other comment that Phil points to, there is no substitute for iteration.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Definitive screening designs - correlated vs. confounded second-order effects
I think you misread my response, I wrote : "there are no aliases (correlations) between main effects, and between main effects and interactions (or quadratic effects), so main effects can be estimated precisely and in an unbiased way."
So indeed, no aliases between main effects and any 2nd order effects, we are on the same page :)
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Definitive screening designs - correlated vs. confounded second-order effects
A further slight correction! Two effects are confounded when their parameter estimates are perfectly correlated. That is to say, the correlation is either -1 or +1. The model matrix's columns used to estimate the parameters are identical (or exactly opposite signs). Including both terms in the model produces a singularity for the solution. They cannot be determined. When two columns in the model matrix have the same values, we say they are both aliases of that column.
The correlations among the estimates of the higher-order terms are not -1 or +1, so they may be simultaneously estimated in the same model, although with inflated variance.
The claim that you referred to at the beginning that a DSD supports the estimation of the full quadratic model for any subset of n factors depends on the projection property of the design matrix. The DSD projects or collapses into a smaller matrix (fewer columns) that exhibits no correlation between any estimates for any n factors. The maximum n for which this property holds depends on the number of factors k and the size of the original DSD.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Definitive screening designs - correlated vs. confounded second-order effects
Hello Mark,
Regarding the last point about DSD projecting into a smaller matrix with no correlation between any estimates for any n factors, I am having trouble understanding this.
I created a 17-run DSD and tried fitting it to only 3 factors. However, when I evaluate this design I see that there is still correlation between the second order parameters. Are you saying that there should be a subset with which there is absolutely no correlation between even 2nd order parameters?
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Definitive screening designs - correlated vs. confounded second-order effects
I cannot find the original paper that describes this property.
The JMP documentation for DSD says: "For 6 through at least 30 factors, it is possible to estimate the parameters of any full quadratic model involving three or fewer factors with high precision." I misquoted the claim in the documentation.
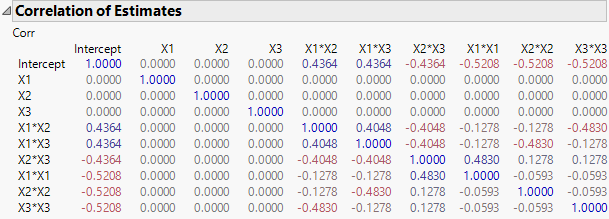
I also created an example of a DSD for this discussion. I added six continuous factors to the design. I simulated the response in which only the parameters for the main effects of X1, X2, and X3 were not 0 to satisfy the condition for the claim. I initially used Fit Definitive Screening to select a model. I clicked Run Model. I clicked Edit under Effect Summary to add all interaction and quadratic terms. Here are the correlations among the estimates:
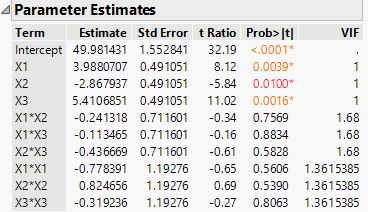
These correlations agree with your finding. All of this information depends only on the design and model matrices, not the response values. Regarding the claim in the documentation, I right-clicked on the Parameter Estimates and selected Columns > VIF:
The low VIF values, which do not depend on the response values, indicate that the correlations should have a small impact on the estimate precision.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us