- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Definitive screening design in the platform "Easy DoE"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Definitive screening design in the platform "Easy DoE"
Hello,
I am using JMP 17 and the new "Easy DoE" platform.
If i'm using "Easy DoE" and a Definitive screening design option, the model will be fitted differently than the "Fit Definitive Screening" method, right?
If so, in such cases where Definitive screening is suitable, is using the Definitive Screening design platform and the unique model fit (and not "Easy Doe") recommended?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Definitive screening design in the platform "Easy DoE"
Hello @O_B,
The designs available in Easy DoE platform are listed here :
Statistical Details for the Easy DOE Platform (jmp.com)
Easy DoE constructs a definitive screening design if all of the following are true:
- There are at least 5 factors
- All factors are either continuous or categorical
- All categorical factors have 2 levels
- There are at most 3 categorical factors
- The number of continuous factors is greater than or equal to the number of categorical factors
For the analysis done depending on the design, you may find your answer here :
Statistical Details for Easy DOE Analyze Tab (jmp.com)
If you switch to "Flexible Mode", you have more details about which modeling platform is used :
Concerning the differences in the modeling platform used, there was a similar question in the Community here : https://community.jmp.com/t5/Discussions/Fit-Definitive-Screening-vs-Stepwise-min-AICC-for-model/m-p...
where I answered about the Fit DSD platform methodology and the possible difference in results.
Different modeling techniques may create slightly different models, but you can evaluate and assess them both statistically and with your domain expertise to choose an appropriate and useful model.
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Definitive screening design in the platform "Easy DoE"
Hello Victor,
Based on your explanation, it appears that the two methods in question are indeed distinct from one another.
Thank you once again for your valuable input.
Oded
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Definitive screening design in the platform "Easy DoE"
Sorry, I may be confused, but there should be no difference in "fit definitive screening designs" regardless of how you get to that analysis. The link posted by Victor was the difference between stepwise and fit model. These are certainly 2 different approaches for building models from data (one being additive and the other subtractive). I personally would not recommend using stepwise for analysis of experimental designs. If your design was properly planned, you should have a model in mind before selecting the design strategy. Now if you are doing data mining, perhaps stepwise is a reasonable approach.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Definitive screening design in the platform "Easy DoE"
Hi @statman,
Sorry if the link provided was a bit confusing.
The question was about the modeling techniques used in the Easy DoE platform, and the link Statistical Details for Easy DOE Analyze Tab states that Fit Stepwise is used in Guided mode, or Fit Least Squares if terms are removed from the model.
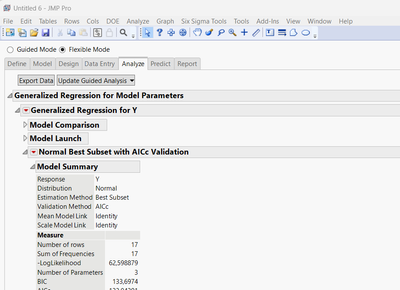
Flexible mode in this platform gives access to other types of modeling, like Generalized Regression with different estimation methods (Forward Selection in JMP, Best Subset in JMP Pro) when there are no Hard or Very Hard to change factors.
"Fit Definitive Screening Design" modeling technique is not used at all in the modeling options of this Easy DoE platform, even if some designs generation (see conditions in my previous answer or in the link provided) may lead to a DSD. In the other Community post, I explained how the Fit DSD is different from other techniques, and may lead to models different than other regression techniques with different estimation methods.
Hope this answer will clarify my response,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us