- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: D-Optimal Mixture Design variable constraints
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
D-Optimal Mixture Design variable constraints
Hello,
i am new to design of experiments and i run into a question. So i researching a mixture System and i have constraits as follows:
0=<A=<25
20=<B=<30
45=<C=<80
and now i would like to augment the design further to the following space
0=<A=<15
15=<B=<20 and
80=<C=<85
so the allowed design space would be something like a polygon. How can i do that in JMP?
- Tags:
- windows
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: D-Optimal Mixture Design variable constraints
Hi @Al_Perr_1988,
Welcome in the Community !
The easiest and most convenient way to augment a design is to use the platform Augment Designs.
This platform enables to add experimental runs to an existing DoE, and enable to do replicates, fold-over, space-filling, increase model complexity, change factors range ...
For your specific example, I created a D-optimal mixture design (for main effects and 2-factors interactions, 12 runs) respecting your constraints so that you can follow the steps.
The original design is created with this script :
DOE(
Custom Design,
{Add Response( Maximize, "Y", ., ., . ), Add Factor( Mixture, 0, 0.25, "A", 0 ),
Add Factor( Mixture, 0.2, 0.3, "B", 0 ),
Add Factor( Mixture, 0.45, 0.8, "C", 0 ), Set Random Seed( 324812 ),
Number of Starts( 30462 ), Add Term( {1, 1} ), Add Term( {2, 1} ),
Add Term( {3, 1} ), Add Term( {1, 1}, {2, 1} ), Add Term( {1, 1}, {3, 1} ),
Add Term( {2, 1}, {3, 1} ), Set Sample Size( 12 ), Simulate Responses( 0 ),
Save X Matrix( 0 ), Make Design}
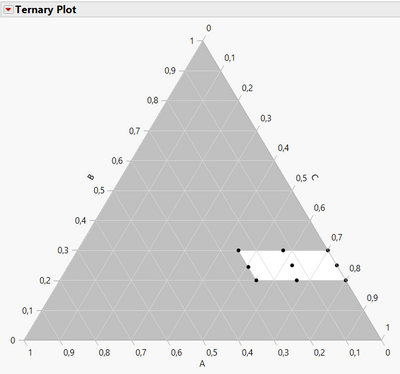
)If we check the experimental space with a Ternary plot, we can see that constraints are respected :
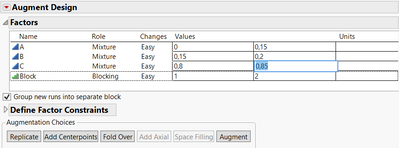
1. From your design table, you can go in the menu "DOE", then "Augment Design". Specify your factors A, B, C and your response(s), and you should have this panel, where you can change the ranges of your factors with the new ones :
2. Click on "Augment", specify the model assumed (main effects, 2-factors interactions, Scheffé Cubic ...) and specify a number of runs or leave the default one (you can try several augmented designs and compare them using the Evaluate Designs platform).
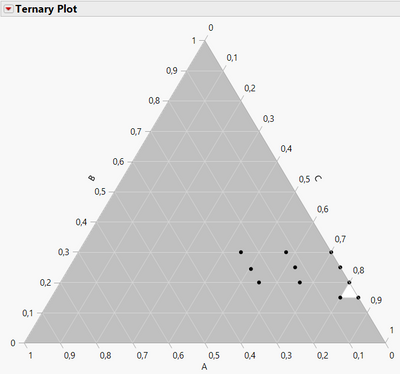
You now have an augmented design with new runs added in your newly defined experimental space that take into account previous information from the original runs.
Here is the script as an example :
dt = Current Data Table();
dt2 = dt << run script( "Original Data Table" );
Current Data Table( dt2 );
DOE(
Augment Design,
X( :A, :B, :C ),
Y( :Y ),
{Group new runs into separate block, Augment Method( Augment ),
Set Random Seed( 1381653403 ), Number of Starts( 67362 ), Add Term( {1, 1} ),
Add Term( {2, 1} ), Add Term( {3, 1} ), Add Term( {1, 1}, {2, 1} ),
Add Term( {1, 1}, {3, 1} ), Add Term( {2, 1}, {3, 1} ), Add Term( {4, 1} ),
Set Sample Size( 20 ), Make Design, Save X Matrix( 0 ), Simulate Responses( 0 ),
Make Table}
);
As you can see, it's quite easy to augment a design.
However, I have some questions for you regarding this new experimental space defined by your new constraints:
With the new constraints, you're in a very small and unexplored area compared to your previous experimental space.
- Is this intended ? Have you checked your constraints ?
- What was the model assumed in the first place ? How many runs ? Why did you choose a D-optimal design ?
- Has the first DoE already be realized and responses measured ?
- What is the precision you can have for measuring the relative quantities of A, B and C ?
- Do you have any idea of the repeatability/reproducibility of your response(s) ?
It looks like the ranges of mixtures factors B and C in this new experimental space seem too narrow to be able to have an informative and robust model.
More info on the context of this DoE and could help us guide you finding an appropriate solution.
I hope this first answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: D-Optimal Mixture Design variable constraints
Hi @Al_Perr_1988,
Welcome in the Community !
The easiest and most convenient way to augment a design is to use the platform Augment Designs.
This platform enables to add experimental runs to an existing DoE, and enable to do replicates, fold-over, space-filling, increase model complexity, change factors range ...
For your specific example, I created a D-optimal mixture design (for main effects and 2-factors interactions, 12 runs) respecting your constraints so that you can follow the steps.
The original design is created with this script :
DOE(
Custom Design,
{Add Response( Maximize, "Y", ., ., . ), Add Factor( Mixture, 0, 0.25, "A", 0 ),
Add Factor( Mixture, 0.2, 0.3, "B", 0 ),
Add Factor( Mixture, 0.45, 0.8, "C", 0 ), Set Random Seed( 324812 ),
Number of Starts( 30462 ), Add Term( {1, 1} ), Add Term( {2, 1} ),
Add Term( {3, 1} ), Add Term( {1, 1}, {2, 1} ), Add Term( {1, 1}, {3, 1} ),
Add Term( {2, 1}, {3, 1} ), Set Sample Size( 12 ), Simulate Responses( 0 ),
Save X Matrix( 0 ), Make Design}
)If we check the experimental space with a Ternary plot, we can see that constraints are respected :
1. From your design table, you can go in the menu "DOE", then "Augment Design". Specify your factors A, B, C and your response(s), and you should have this panel, where you can change the ranges of your factors with the new ones :
2. Click on "Augment", specify the model assumed (main effects, 2-factors interactions, Scheffé Cubic ...) and specify a number of runs or leave the default one (you can try several augmented designs and compare them using the Evaluate Designs platform).
You now have an augmented design with new runs added in your newly defined experimental space that take into account previous information from the original runs.
Here is the script as an example :
dt = Current Data Table();
dt2 = dt << run script( "Original Data Table" );
Current Data Table( dt2 );
DOE(
Augment Design,
X( :A, :B, :C ),
Y( :Y ),
{Group new runs into separate block, Augment Method( Augment ),
Set Random Seed( 1381653403 ), Number of Starts( 67362 ), Add Term( {1, 1} ),
Add Term( {2, 1} ), Add Term( {3, 1} ), Add Term( {1, 1}, {2, 1} ),
Add Term( {1, 1}, {3, 1} ), Add Term( {2, 1}, {3, 1} ), Add Term( {4, 1} ),
Set Sample Size( 20 ), Make Design, Save X Matrix( 0 ), Simulate Responses( 0 ),
Make Table}
);
As you can see, it's quite easy to augment a design.
However, I have some questions for you regarding this new experimental space defined by your new constraints:
With the new constraints, you're in a very small and unexplored area compared to your previous experimental space.
- Is this intended ? Have you checked your constraints ?
- What was the model assumed in the first place ? How many runs ? Why did you choose a D-optimal design ?
- Has the first DoE already be realized and responses measured ?
- What is the precision you can have for measuring the relative quantities of A, B and C ?
- Do you have any idea of the repeatability/reproducibility of your response(s) ?
It looks like the ranges of mixtures factors B and C in this new experimental space seem too narrow to be able to have an informative and robust model.
More info on the context of this DoE and could help us guide you finding an appropriate solution.
I hope this first answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: D-Optimal Mixture Design variable constraints
Hello Victor,
i have realized a part of the DoE. Well the problem ist that the space is narrowed down by the producability of the Material in the production parameters we wanna use. So i am basically checking the producability and creating the design according to that. The problem is that there is no literature for the problem we are trying to solve because the process is patented.
So what i did is:
i started with with the constraints
7=<A=<20
20=<B=<25 and
55=<C=<73
according to what my predecessors researched. To this plan i measured responses with 12 runs. I then augmented to the design i shared before with 9 additional runs and now i want to research the final space. The repeatability of the measurement of the response is within 5-10% and the for the relative quantities i have a lab scale which is precise to micro-gram.
My problem is if this augmentation is mathematically sound. I did exactly the same things you undertook. Thanks for your input!
Greetings from Germany
Alex
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: D-Optimal Mixture Design variable constraints
Hello Victor,
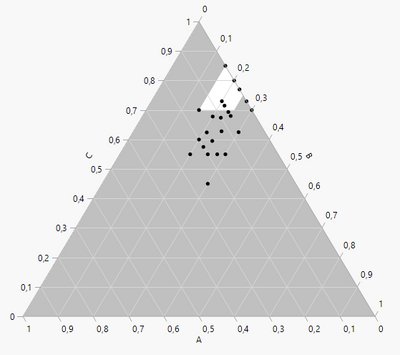
i seem to have overlooked one of your questions, the model assumed was the Scheffe cubic model. I chose D-Optimal design based on literature recommendations for mixture designs with constraints. I expanded the space to :
0=<A=<15
15=<B=<25
70=<C=<85
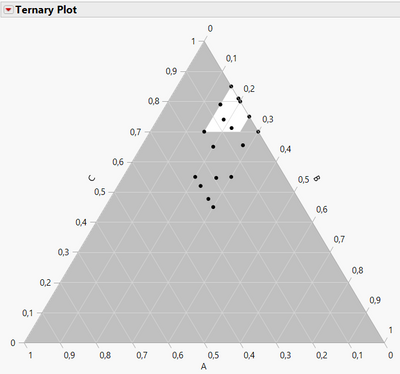
And my ternary diagram looks something like this :
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: D-Optimal Mixture Design variable constraints
Hi Alex,
Thanks a lot for the answers and details provided.
I was curious about the final experimental space (which looked very small and totally disconnected from your initial experimental space, and so not benefiting from your initial information gathered by the experiments), but with the constraints you mentioned in your last reply (with broader ranges for B and C than in your initial post), I have the same experimental space and a similar design :
I imagine you had interesting results in the corner of your initial experimental space ( A between 0 and 7%, B between 20 and 25% and C between 70 and 80%) which leads you to investigate a closer experimental area with lower A, lower B and higher C proportions/ratio.
It makes sense, thanks for the clarification, details and corrections !
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us