Correlation between an ordinal output variable and a continuous predictive variable

[#1]

Hello Community,

I have a question about a case of finding out whether there is any important correlation between an ordinal response variable and a continuous predictive variable.

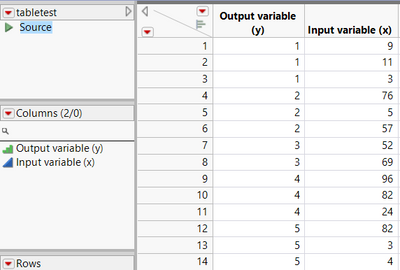
This is my data (I also attach the JMP file just in case):

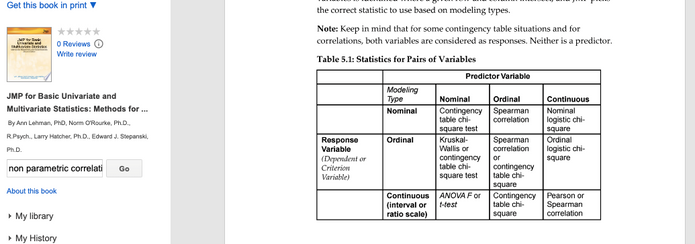
At first I thought of using “Fit model platform” and then displaying Spearman’s coefficient, but then I found this information in a JMP book:

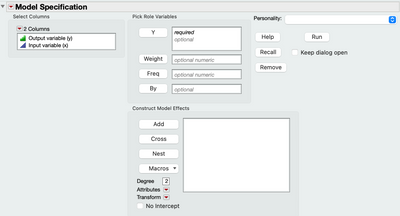
According to this table, when dealing with an ordinal response variable and a continuous predictive variable, I should work with ordinal logistic. I conducted this in the “Fit model” platform and it gave me these results (script present in the file attached):

I had to go through several sources of JMP documentation and videos to try to understand these results. I found a lot of sources, but most of the time they focused on nominal logistic cases and were too focused on describing each part of the report rather than on practical meaning and most useful information to get from this. My objective is not to have an in-depth understanding of the math/stats, but rather be very practical on what these results are telling me.

What I could understand (please correct me if I’m wrong) is that the value with the green circle in the figure above tells me that my model is not very good. For my case, using a single input variable, could I use this result to finally say that there is not any sort of correlation or association between my input and output variables ? > this is the main question I want to answer.

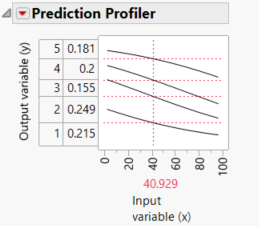
I was also interested in understanding the results of the prediction profiler:

Are the proportions in the Y axis telling me the percentage of probability of having a value of 1, 2, 3, 4 or 5?

Finally, too short questions that are somewhat related to this topic:

a) In the case of having a Likert scale (intensity scale) for my output variable, I know that it is mostly an ordinal variable and therefore to be treated with ordinal logistic too. However, If I have several measurements for each single trial (row) and I average the values, now the result begins to look like a continuous number. Could in this case treat those means as a continuous variable (instead of ordinal)?

b) If my output variable are frequency values. Is it better to treat it as ordinal variable or could I treat it as a continuous variable.

Thanks for reading,

Julian

[#2]

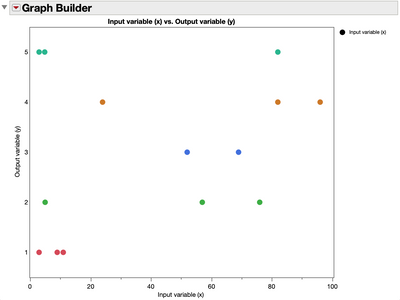
Your output (y) variable is very noisy if you were expecting the x to accurately predict your y. Level 5 of the y variable has two out of three x-values that look more like the x-values of when y=level 1, i.e. two level 5 results are associated with x-values of 3 and 4 making it look more like level 1 of your y-variable which has x-values of 9, 11, and 3. Levels 2 and 4 of your y-variable similarly span a wide range of x-values (from 5 to 76 for level 2 and from 24 to 96 for level 3). As your analysis confirms x is not a statistically significant predictor of y. Is there another potential input variable not yet measured that could be influencing your y-variable? 

Your statement of how to interpret the prediction profiler for an ordinal logistic regression model is correct. But please refrain from trusting these predictions as x is not a significant predictor of y due to the excessive noise in the relationship.

Regarding your scenario a). Are these several repeat measurements of the same thing? If so, what does the mean and variance of these repeat measurements look like?

Regarding scenario b). What are you measuring the frequency of? This may be another variable that should be recorded which would take either a x or y role in the analysis with the frequency data assigned a weight or frequency role.

[#3]

Hi @malcolm_moore1 ,

Thank you very much for your answers. I forgot to mention that it was not real data, I just created random numbers to be able to illustrate my case. However, I understood your point for the main question. Concerning the two scenarios, to be honest, I did not understood very well. I think that providing a more illustrated example could make my point clearer.

a) In the picture below, I present not real data about two Y variables (saltiness and Y2). Initially, saltiness is evaluated by an ordinal scale, but as you see in the picture, if several people participate and I average these notes, the average looks more like a quantitative continuous variable. Therefore, I was wondering if to evaluate correlation between average of saltinees and variable Y2, I could use normal regression (no ordinal  logistic regression  despite that saltiness was originally an ordinal variable)

b) For the frequency case, I'm gonna use the same two variables (saltiness and Y2), but let's now supose that the data I have for saltiness is measured as the percent of the people who found the specific product as salty. I present this in the picture below (data invented).

Now suppose I want to evaluate if there is a correlation between saltiness (measured in frequency) and Y2 (normal quantitative variable). is saltiness a quantitative continuous type of variable and therefore I could use a normal regression to evaluate correlation? or due to the fact that saltiness is a frequency I should consider rather as an ordianl variable for the correlation analysis? I ask you this since it seems that frequencies are tricky and I have not been able to find clear information about this.

Thank you for reading,

Julian

[#4 · Accepted solution]

You should be fine treating your average of three measurements as a continuous variable. See the attached data to illustrate this. I've simulated three columns of 100 observations from an integer measurement in the range 1 to 10. If you run the distribution script you will see that the best fitting distribution of the average of the three integer measurements is a normal distribution (confirmation of the central limit theorem coming into play, which basically states the average of many measurements will be normally distributed even if the observations themselves are sampled from a non-normal distribution). Just be careful to not reduce the number of repeat measurements to below 3. 

Regarding your second case, then providing your percentage measurement falls within the range 10% to 90% you should be safe treating it as a (linear) continuous predictor. Any relationships with your y-variable could be modelled with standard regression analysis methods. If however your percentage measurement has values outside the range 10% to 90% then non-linear relationships with your y-variable are more likely to occur. Making it critical to graph the data to determine if any non-linear terms need to be included in your regression model. Remembering the regression model is an empirical approximation of the trend in your data and not a mechanistic model.

[#5]

Thank you very much @malcolm_moore1 . Your explanations have really helped me to better understand how to deal with these situations