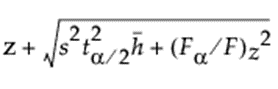- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Confidence interval in Fit Model Actual by Predicted plot
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Confidence interval in Fit Model Actual by Predicted plot
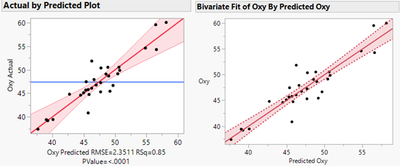
I would like to know how the confidence interval in Fit Model Actual by Predicted plot is calculated. I tried to manually plot Actual vs Predicted with Fit Y by X and the confidence interval is different with the one in Fit Model. I can manually calculate the confidence interval of Fit Y by X but cannot figure out how to calculate the one in Fit Model. Please advise. Thanks a lot!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confidence interval in Fit Model Actual by Predicted plot
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confidence interval in Fit Model Actual by Predicted plot
Hi @vcl0124 :
Q:I found the z^2 in below equation should be (z - mean of predicted)^2. Do you agree?
A: not according to Sall (1990). See JMP reference
https://www.jstor.org/stable/2684358
https://blogs.sas.com/content/iml/2022/07/11/confidence-bands-partial-leverage-plot.html
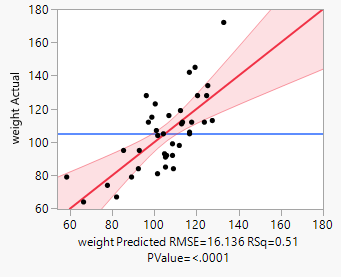
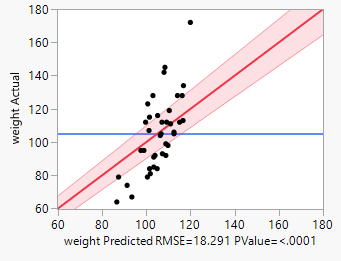
Q: I believe the interception one is the better model but the leverage plot is wider. How to understand this? Please advise.
A: This may be a bit involved for this forum; but , briefly, unless you have a really good reason to exclude the intercept, do not exclude it. The second plot you show, clearly shows the model is not correct so any inference drawn from that is not correct as well.
Here is a pretty good discussion(s).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confidence interval in Fit Model Actual by Predicted plot
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confidence interval in Fit Model Actual by Predicted plot
Hi MRB3855,
Thanks a lot for your advice! However, I found the z^2 in below equation should be (z - mean of predicted)^2. Do you agree?
Another question is about fit model with (1st plot below) and without (2nd plot below) interception. I believe the with interception one is the better model but the leverage plot is wider. How to understand this? Please advise. Thanks a lot!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confidence interval in Fit Model Actual by Predicted plot
Hi @vcl0124 :
Q:I found the z^2 in below equation should be (z - mean of predicted)^2. Do you agree?
A: not according to Sall (1990). See JMP reference
https://www.jstor.org/stable/2684358
https://blogs.sas.com/content/iml/2022/07/11/confidence-bands-partial-leverage-plot.html
Q: I believe the interception one is the better model but the leverage plot is wider. How to understand this? Please advise.
A: This may be a bit involved for this forum; but , briefly, unless you have a really good reason to exclude the intercept, do not exclude it. The second plot you show, clearly shows the model is not correct so any inference drawn from that is not correct as well.
Here is a pretty good discussion(s).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confidence interval in Fit Model Actual by Predicted plot
Hi MRB3855,
Thanks a lot for your advice!
For z^2 or (z - mean of predicted)^2, I cannot read the paper. However, the example in the 2nd link seems to have mean of predicted = 0. Actually, if you look at the shape of the leverage plot of the with interception case, the confidence interval is the smallest at mean of predicted. Therefore, z^2 must be smallest at mean of predicted and that's why I suspected the z is shifted by mean of predicted (replace z by z - mean of predicted).
For the leverage plot of without interception, I figured out it is tested against y=0 instead of y=mean of y and that's why the confidence interval is narrower as y=0 is very unlikely. I actually think it is OK to test without interception model against y=mean which should give us more meaningful information about whether the model is valid, am I correct?
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us