- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Confidence interval for degradation data analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Confidence interval for degradation data analysis
Hello,
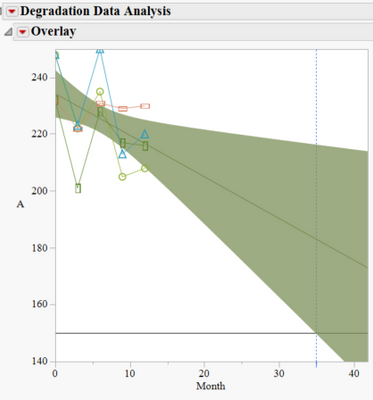
In degradation analysis, is there any option to save the crossing time with 95% confidence interval. Confidence interval is shown in the plot but I do not see it mentioned anywhere in the report. Is there any option to get those numbers. Below is the plot from degradation data analysis showing the crossing time with 95% CI.
Thank you.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confidence interval for degradation data analysis
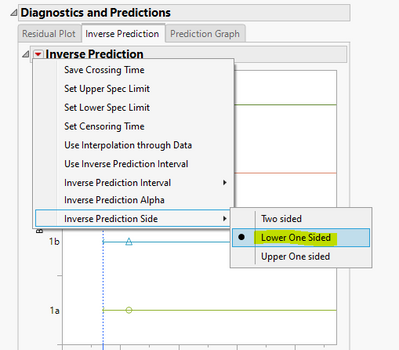
I understand now. You are using "Stability Analysis" part of the platform. Stability analysis is a special application of the general degradation analysis. Its behavior is tailored to suit the special need of stability analysis. The "Prediction" column that you see is already the crossing time of the confidence interval line with the threshold. And it is lower one-sided. The actual crossing times of the degradation lines with the threshold are not reported, because they are not the interest of stability analysis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confidence interval for degradation data analysis
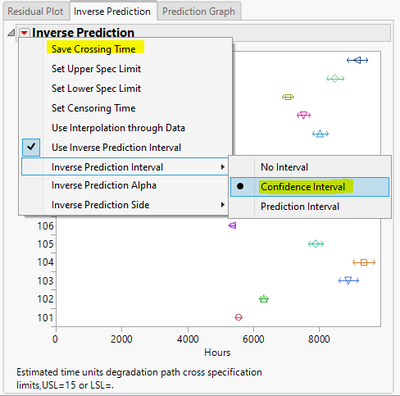
Try to select "Confidence Interval" in Inverse Prediction, then select "Save Crossing Time". See whether that is what you need.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confidence interval for degradation data analysis
@peng_liu Thank you for your reply. I tried this solution but it just saves the predicted crossing time not the confidence interval.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confidence interval for degradation data analysis
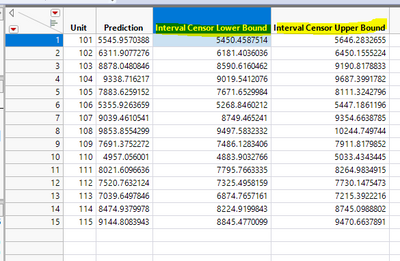
That's odd. The following data table is what you should see. The two highlighted columns are where confidence interval bounds cross the threshold. If you don't see them. There is something I don't understand. You may either post more details here, or you may contact support@jmp.com if it is inconvenient to discuss here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confidence interval for degradation data analysis
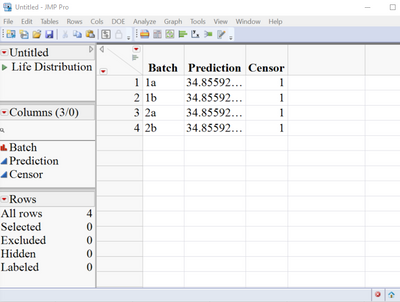
@peng_liu I attached the data table and below is snapshot of what I get when I go to Inverse Prediction > Save Crossing Time.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Confidence interval for degradation data analysis
I understand now. You are using "Stability Analysis" part of the platform. Stability analysis is a special application of the general degradation analysis. Its behavior is tailored to suit the special need of stability analysis. The "Prediction" column that you see is already the crossing time of the confidence interval line with the threshold. And it is lower one-sided. The actual crossing times of the degradation lines with the threshold are not reported, because they are not the interest of stability analysis.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us