- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Calculation of t-distribution, JMP 13
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Calculation of t-distribution, JMP 13
Hello,
I would like to knwo, how the t-distribution is calculated in the programm. The results I got from the programs are different with the results I calculated by myself, with the help of methods, mentioned in various books and scientific researches.
In addition I would like to know, how it is possible to set up an own quantil in the t-distribution. When I make a box plot, I just can change it in the standard normal distribution.
My calculation way is
n = 4
calculate mean and variance
calculate c = value from table http://www.sjsu.edu/faculty/gerstman/StatPrimer/t-table.pdf for a 95% each side
df = n-1
(c*root(variance))/(root(n))=k
mean+-k = result
Thanks for you ideas,
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculation of t-distribution, JMP 13
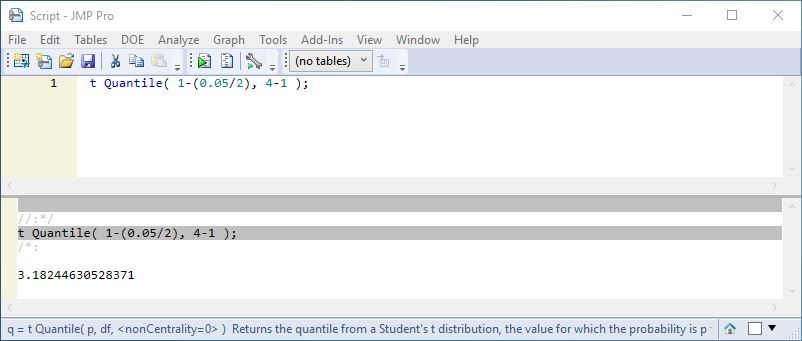
You are calculating a two-sided confidence interval for the mean using the quantile from the t distribution for (1-alpha)% confidence and (n-1) degrees of freedom. The function for this in JMP is t Quantile( probability, df ). Here is the quantile for a two-sided 95% confidence interval for the mean:
I used the script editor and an embedded log but you could also enter it into a column as a formula. This quantile is correct.
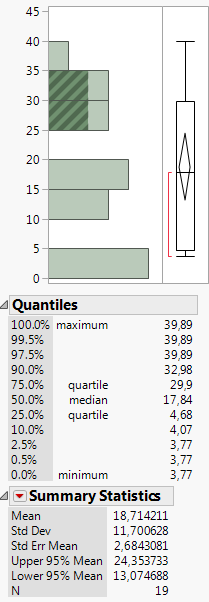
If you enter your 4 observations into a column, then select Analyze > Distribution, select the data column and click Y, Columns, then click OK. You will find the 95% CI in the Summary Statistics report.
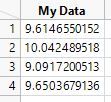
Here is an example of 4 observations:
Here is the Summary Statistics report for them:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculation of t-distribution, JMP 13
I suspect that you are having a mismatch of t-tests, in that you may be comparing a t-test for unequal variances, with a t-test for equal variance. You can get the details of what JMP is doing from it's documentation
Help==>Books==>Basic Analysis==>The t-test Report
Here is a cut and paste from that document
The t-test Report
Note: This option is applicable only for the Means/Anova/Pooled t option.
There are two types of t-Tests:
• Equal variances. If you select the Means/Anova/Pooled t option, a t-Test report appears.
This t-Test assumes equal variances.
• Unequal variances. If you select the t-Test option from the red triangle menu, a t-Test
report appears. This t-Test assumes unequal variances.
The t-test report contains the following columns:
t Test plot Shows the sampling distribution of the difference in the means, assuming the null
hypothesis is true. The vertical red line is the actual difference in the means. The shaded
areas correspond to the p-values.
Difference Shows the estimated difference between the two X levels. In the plots, the
Difference value appears as a red line that compares the two levels.
Std Err Dif Shows the standard error of the difference.
Upper CL Dif Shows the upper confidence limit for the difference.
Lower CL Dif Shows the lower confidence limit for the difference.
Confidence Shows the level of confidence (1-alpha). To change the level of confidence, select
a new alpha level from the Set Level command from the platform red triangle menu.
t Ratio Value of the t-statistic.
DF The degrees of freedom used in the t-test.
Prob > |t| The p-value associated with a two-tailed test.
Prob > t The p-value associated with a lower-tailed test.
Prob < t The p-value associated with an upper-tailed test.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculation of t-distribution, JMP 13
Thanks for the information
Apparently, there is no formular given. I found in a math book different ways to handle the t-test. I need the results to be the same.
Is it possible to draw boxplots with my calculated data in JMP? Otherwise I need to look for a new programm.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculation of t-distribution, JMP 13
You are calculating a two-sided confidence interval for the mean using the quantile from the t distribution for (1-alpha)% confidence and (n-1) degrees of freedom. The function for this in JMP is t Quantile( probability, df ). Here is the quantile for a two-sided 95% confidence interval for the mean:
I used the script editor and an embedded log but you could also enter it into a column as a formula. This quantile is correct.
If you enter your 4 observations into a column, then select Analyze > Distribution, select the data column and click Y, Columns, then click OK. You will find the 95% CI in the Summary Statistics report.
Here is an example of 4 observations:
Here is the Summary Statistics report for them:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculation of t-distribution, JMP 13
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculation of t-distribution, JMP 13
No, of course not.
You enter your data into a JMP data table and then use one of the platforms in the Analyze menu. The confidence intervals for the mean in Distribution, the slope in Bivariate (Fit Y by X), tests in Oneway (Fit Y by X), and all the platforms through the platforms launched by Fit Model will calculate the confidence limits automatically. (It sounds like each of your 'experiments' is a sample drawn for a different population and you want a new confidence interval for the mean, so Distribution will do it for you.)
There is no need for you to look up the t quantile or calculate the intervals by hand.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculation of t-distribution, JMP 13
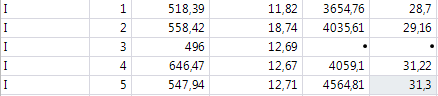
I was doing some experiments but many samples got damaged, thats why the number varies.
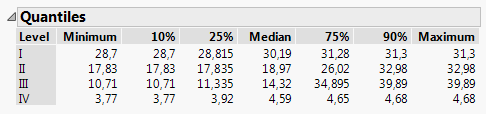
I have done the boxplots but the only data I can get out of it is like shown in the picture
But I need the Minimum, 5%, mean, 95%, Maximum, variance, standard deviation
Leftclick on the chart let me "format column", but after click "ok" nothing changes.
How can I change that?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculation of t-distribution, JMP 13
The quantiles in the report that you show are fixed. You could enter the same data in the Distribution platform and put the factor column in the By role. This launch will give the the quanitile and mean information for each level separately.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculation of t-distribution, JMP 13
How can I make an empty cell, wish is not calculated for the quantiles? So far I get wrong values. E.g. for the last column the mean is about 18 but all results are higer, so there must be a mistake.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculation of t-distribution, JMP 13
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us