- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Calculating 95% Confidence Intervals for a Standard Beta
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Calculating 95% Confidence Intervals for a Standard Beta
Hi everyone,
I am doing an analysis where I need to report Standard Betas and their 95% confidence intervals. When I run a regression model, JMP will give me the Standard Beta itself, but the confidence intervals listed next to it refer to the estimate and not the beta itself.
I understand that I can get the CIs by creating a new standardised variable first and then running the analyses with this variable instead - after which the CIs will refer to the beta - but this is a bit fiddly, especially since I am working with a lot of variables.
Is there any easier way to do this in JMP? Alternatively, would it be possible to rig up an excel sheet to do this for me? I have been playing around with it, and dividing the standard beta by its estimate and then multiplying the result by the 95% CIs seems to get very close - usually within a few decimal places - but it's slightly off and I am wondering why.
Any help you can give me would be greatly appreciated. Thanks!
P.S. - Is there a way to make the standard beta display by default? I can do it with the CIs, but seemingly not with the standard beta.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculating 95% Confidence Intervals for a Standard Beta
@Debaser I did not find any JSL message to compute and report Confidence Intervals for Std Beta. My experience is more with scaled factors and estimates, so I did a little internet search for this topic. There seems to be a bit of discussion on best methods for these confidence intervals. I liked this paper Computing Confidence Intervals for Standardized Regression Coefficients. This paper's conclusion from their simulated deviant models is "we recommend the delta method (Yuan & Chan, 2011) or a nonparametric bootstrap (Efron & Tibshirani, 1998)."
My search of this topic was not extensive, so it will be interesting to hear from the JMP technical experts. Using this paper as my support, the script below uses the wonderful Bootstrap() methods provided by JMP to compute the Std Beta lower and upper 95% limits. Bootstrapping takes time and this script does 1000 iterations. You might want to reduce this to 500.
See the attached script. I have only tested it on JMP 14. If you have a different version, please specify.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculating 95% Confidence Intervals for a Standard Beta
@Debaser I did not find any JSL message to compute and report Confidence Intervals for Std Beta. My experience is more with scaled factors and estimates, so I did a little internet search for this topic. There seems to be a bit of discussion on best methods for these confidence intervals. I liked this paper Computing Confidence Intervals for Standardized Regression Coefficients. This paper's conclusion from their simulated deviant models is "we recommend the delta method (Yuan & Chan, 2011) or a nonparametric bootstrap (Efron & Tibshirani, 1998)."
My search of this topic was not extensive, so it will be interesting to hear from the JMP technical experts. Using this paper as my support, the script below uses the wonderful Bootstrap() methods provided by JMP to compute the Std Beta lower and upper 95% limits. Bootstrapping takes time and this script does 1000 iterations. You might want to reduce this to 500.
See the attached script. I have only tested it on JMP 14. If you have a different version, please specify.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculating 95% Confidence Intervals for a Standard Beta
p.s. The paper also includes R code for their recommended calculations. JMP can call R, but I did not go down that path if you are not an R user (do not have it installed).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculating 95% Confidence Intervals for a Standard Beta
Hi there,
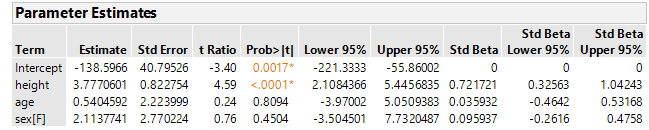
Thanks so much for this! This seems to be exactly what we're looking for. We're using JMP 14.1, but for some reason, the script will not function properly. I am not sure if we're just not using it correctly.
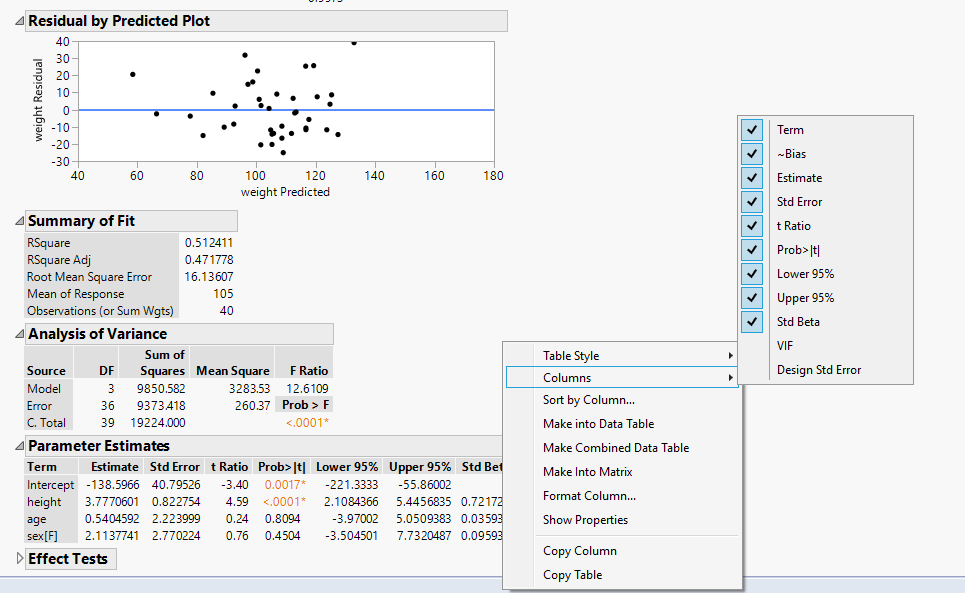
The data file opens as expected, but the columns for the standard beta CIs are not displayed for some reason when I run the script. This is without making any modifications to have it work on my own table - just using the "Big Class" example table. I suspect I am making some kind of amateur error here. I've attached a screenshot of the output I get. Do you have any idea what I might be doing wrong?
Thanks again for all the help, I really appreciate it!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculating 95% Confidence Intervals for a Standard Beta
First of all, when I run the script and the confidence intervals appear in the display tabl, when I use the interface to look at the columns those new column will not appear, because the interface you used is built-in and only lists the built-in columns.
Second, I have JMP Pro 14.1. From the online help, it seems Bootstrap is only available on JMP Pro. That might be the issue.
If you have JMP PRO, to determine the error, I'd need to see the log. To view the log, CTRL+SHIFT + L. Right click and select Clear Log, then run the script again. The Log should report any error.
A script can be run to perform a bootstrap:
- randomly select from the input, capture the Std Beta
- compute intervals from the distribution.
If I get some open time in the next few days, I'll write the script. But maybe someone has built an app to do that and will respond.
Sorry, I should have mentioned JMP PRO.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculating 95% Confidence Intervals for a Standard Beta
Ah, so there's my problem! I'm using the normal version of JMP, not the Pro edition.
Is there any way to do this without bootstrapping, or am I out of luck?
Thanks again!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculating 95% Confidence Intervals for a Standard Beta
Debaser,
I know how to write a script that uses the Fit Model Interface and captures the model and the window, so there are two options:
- Add code to do the bootstrapping (which requires sampling with replacement and running the model repeatedly). I am concerende this could be very slow.
- Add code to compute the delta method proposed in the article that I referenced.
Of course, the alternative is to add the calculations the reference article demonstrated as accurate only of the model assumptions are strictly true.
I have not studied the delta method algorithm. I'll respond to this post in a few days to see if any of these methods work without too much of a performance hit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Calculating 95% Confidence Intervals for a Standard Beta
I know how to write a script that uses the Fit Model Interface and captures the model and the window, so there are two options:
- Add code to do the bootstrapping (which requires sampling with replacement and running the model repeatedly). I am concerened this could be very slow.
- Add code to compute the delta method proposed in the article that I referenced.
Of course, the alternative is to add the calculations the reference article demonstrated as accurate only if the model assumptions are strictly true.
I have not studied the delta method algorithm. I'll respond to this post in a few days to see if any of these methods work without too much of a performance hit.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us