- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Bezier interpolation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Bezier interpolation
Hi,
Is there a function to plot Bezier interpolation?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Bezier interpolation
http://users.umiacs.umd.edu/~ramani/cmsc460/Lecture9_interp_2008.pdf says

I suspect 1 or 4 might apply here; I'm beyond my knowledge.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Bezier interpolation
@Craige_Hales and @mitulshah ,
My knowledge and experience of Bezier curves is limited. I have seen their utility in drafting (construction and landscaping) design and clothing design. Of course, mathematical underpinnings always is interesting to me. I did a little noodling around the internet and found that @mitulshah's quest for Excel's Bezier spline, B-spline, algorithm is a common one. One link Excel Smoothing Algorithm question included the link to a zip file: http://xlrotor.com/Smooth_curve_bezier_example_file.zip This zip contains a 2002 .xls example of a Bezier curve with embedded automation routines to grab the pixels from the Excel smoothed curve and interpolate teh points on the curve. It is not "exact" and uses a technique that grabs 4 pixels off the curve. The endpoint is used twice in the first interpolated point and the last interpolated point.
One JMP discovery I made after Craige's post about the GraphBuilder Line element option to make it a curve, is the spline used for this platform must use a different algorithm because the endpoint slopes are very similar to Excel's. i started a script to do some DSP (digital signal processing) by extracting the pixels of the GB plot. Then I found the web links listed above, and decides to just use the interpolated points from the Excel spreadsheet and overlay it with the GB Line(curve). The first screenshot below depicts the Excel worksheet with the Excel graph with Bezier spline and interpolated points, which were added as Spin B points to the JMP table. The second picture shows the JMP GB Line(curve) with the Excel interpolated points overlaid.
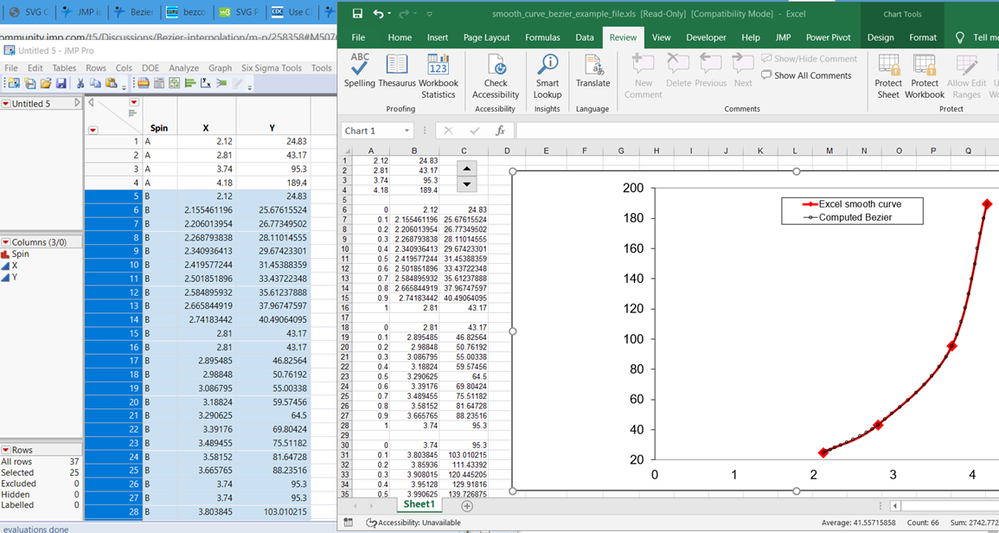
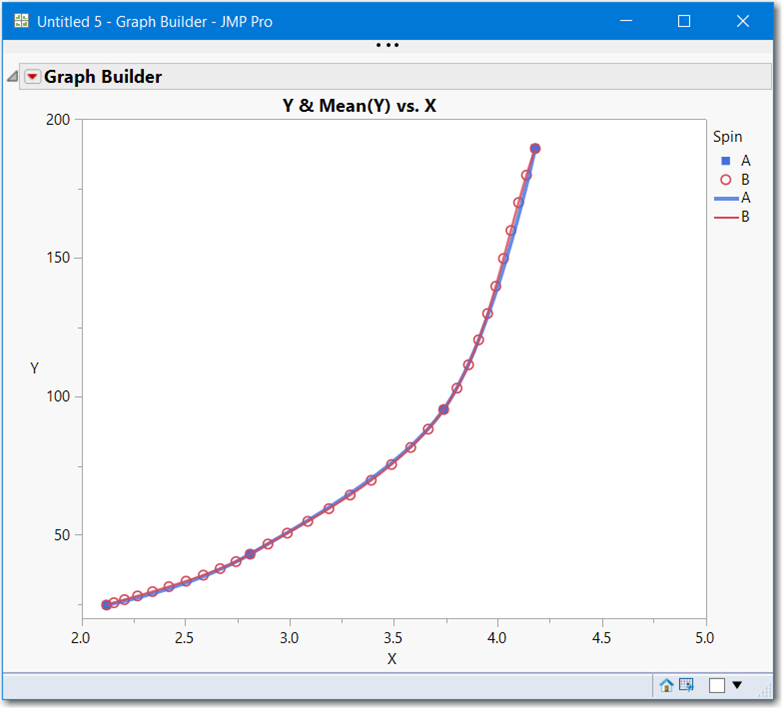
You'll notice the interpolations are slightly offset from the JMP Line(curve) on the upper tail, that could be due to the interpolation algorithm, differences in Excel and JMP curves or a combination of both. Note in those same 4 points are slightly higher than the the curve in the Excel chart.
So, my conclusion is that the JMP GB Line(curve) spline is very similar to the Excel Bezier curve. My interest is not high, but if I get bored I might finish my DSP script to "get" the Line(curve) points. Earlier versions of JMP used to report curve points in saved .jrn files,now just a reference to a hidden function is in the .jrn file.
Now, if I were consulting on this problem, my first set of questions would be:
- Where do these data (4 points) come from and what is the goal?
- Spline curves, like lines and polynomials, can be useful to create calibration curves (curves to be used for interpolation) in place of complex functional relationships. However, for accuracy purposes, regular data intervals and replication is recommended, if interpolations are to be calculated from the curves. Since the X values are irregularly spaced, I wonder if there is a third (or more) variable influencing both X and Y. For example, both are readouts from a daily or weekly test readout.
- Is there a fundamental, first principle, underpinning with the relationship of X and Y, for example: dose response; cell growth; contamination-corrosion, etc.
- Why so few points? What's the cost of replicaton?
It is my experience that if there is a fundamental underlying nonlinear relationship, it is often worth the effort of getting the data and fitting the relationship to estimate the parameters (learning curves, degrdation curves), etc. As found in the excellent information provided by Craige Hales, small differences in the control points (number and location), knots and end points can make big differences in the curvature (points on the curve) of a spline, especially with wide gaps in "x". It is my hunch that Excel purposely did not publish points or a formula for their curve spline so people would not use it like a fitted model for estimation. Note with "close" values of X and replication, interpolation is much less risky.
- « Previous
-
- 1
- 2
- Next »
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us
