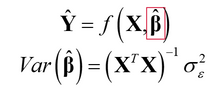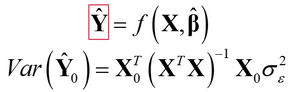- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Augmented design with diffrent optimality criteria
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Augmented design with diffrent optimality criteria
I have 4 continuous factors. I made an custom Design with recommended optimality which is d for a model containing main effects, 2nd order interractions and 2nd order powers. I run 80 Experiments and use least square estimate for linear model. Then i see that i have to include 3rd order powers to my model and i made augmented Design with I optimality by including 3rd order powers to my model.
Now i wonder that augmented Design with I optimality can be use With custom Design with d optimality? Does this combination work well?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Augmented design with diffrent optimality criteria
This approach will work fine. But I think a few clarifications are in order. I do have questions, such as how did you determine that you needed cubic terms? And do the cubic terms make sense from a physical science/process point of view? To name just a few. But I trust that you had good reasons to add the cubic terms to the model, so I will set those questions aside and try to answer yours.
D-optimal designs are optimal for estimating the parameters of your model. In other words, they will minimize the standard errors of the parameter estimates.
I-optimal designs are optimal for prediction. They will minimize the integrated variance of the prediction error.
Although D-Optimal designs are best at estimating parameter estimates, they still predict very well. The prediction errors will only be slightly higher than an I-optimal design. These designs do not guarantee orthogonality as that is not part of the optimization criteria. They are the default designs in JMP UNLESS you click the RSM button to build the model. When you click that, JMP will switch to I-Optimality. Notice that if you build the RSM model by clicking the cross button and the powers button rather than RSM, the default will remain D-optimal.
Although I-Optimal designs are best at predicting, they still do a good job of estimating the parameters. The parameter errors will only be slightly larger than those from a D-optimal design. The I-optimal designs do not guarantee orthogonality either as that is not part of the optimization criteria.
So all of this means that the user should choose the optimality that best meets their needs. There is no such thing as "the best" design. The "best" design will depend on the researcher's objectives and wants/needs from the design. Those are determined by people, not statistics. Therefore, different opinions can lead to different designs and design approaches. After all, someone could say that you should have only created one design and not augmented the original design. I don't believe that, but I hope you see the point. The design creation process utilizes the science knowledge of the experimenter as much or more than it utilizes the statistical/mathematical properties of a design.
So is the approach that you outline of a D-Optimal augmented with I-optimal a valid approach? Absolutely. Is it the best? That will depend on YOUR needs. I can tell you that it is a fine approach and you should get a design with good mathematical properties. The resulting design would not have as good of a D-optimality criteria as if you had created the entire design using D-optimality. The resulting design would likely not have as good of an I-optimality criteria as if you had created the entire design using I-optimality. But that is okay, as long as the design meets your purposes and allows you to build a good model that answers your questions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Augmented design with diffrent optimality criteria
I am glad that my explanation helped some.
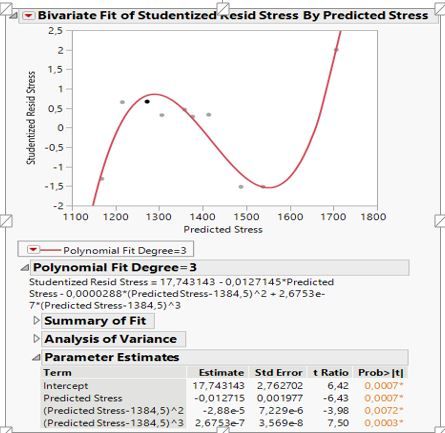
When it comes to the cubic term, what does a plot of the raw data versus the factors look like? Knowing the science behind your data, does it make sense that you would see a cubic relationship? It looks like you have one point that was not predicted well when the prediction of stress was near 1700. Have you verified that the data is real and not an outlier? Cubic terms do not appear that often, so people often question when they do appear. But it very well could be real, and based on your residual plot, I understand why you added a cubic term.
As for the D and I-optimality stuff, it is easy to think that the most precise parameter estimates (D-optimal) will naturally lead to the lowest prediction error (I-optimal), but that is not necessarily the case. Consider the case of only one predictor variable, X, and a total of 9 runs. If I want a quadratic model, we will need to study 3 levels of X. If I want the best possible parameter estimates, I would put 3 runs at the lowest setting for X, 3 runs at the middle setting, and 3 runs at the highest setting. I need to put more runs at the extremes to better model that linear term. This is what a D-optimal design does.
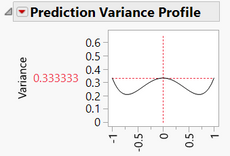
What about for prediction error? Well, prediction error is "minimized" somewhere between the low and mid settings and again somewhere between the mid and high settings:
How could I get rid of the hump in the middle? Move some points from the ends to the middle. This is what the I-optimal design does. It uses two points at the ends of the X-range and places 5 points in the center. This will lower the prediction variance in the center, but the ends will be raised.
Remember, I-optimal is for integrated variance, so the "area under the curve" is minimized this way. This is why when people are trying to optimize a process, they want the optimum to be somewhere near the middle of the design space because an I-optimal design provides the best predictions in that area.
If you like mathematics and matrix algebra, remember that your model is:
D-optimal designs work on minimizing Var(B-hat).
The I-optimal designs focus on the left-side of that equation. Specifically,
and minimize the integrated variance of Y-hat. Notice that the variance in this formula is for a specific point of your inputs (X sub-0). The variance is calculated over the entire design space and integrated for I-optimal designs.
I hope this helps.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Augmented design with diffrent optimality criteria
This approach will work fine. But I think a few clarifications are in order. I do have questions, such as how did you determine that you needed cubic terms? And do the cubic terms make sense from a physical science/process point of view? To name just a few. But I trust that you had good reasons to add the cubic terms to the model, so I will set those questions aside and try to answer yours.
D-optimal designs are optimal for estimating the parameters of your model. In other words, they will minimize the standard errors of the parameter estimates.
I-optimal designs are optimal for prediction. They will minimize the integrated variance of the prediction error.
Although D-Optimal designs are best at estimating parameter estimates, they still predict very well. The prediction errors will only be slightly higher than an I-optimal design. These designs do not guarantee orthogonality as that is not part of the optimization criteria. They are the default designs in JMP UNLESS you click the RSM button to build the model. When you click that, JMP will switch to I-Optimality. Notice that if you build the RSM model by clicking the cross button and the powers button rather than RSM, the default will remain D-optimal.
Although I-Optimal designs are best at predicting, they still do a good job of estimating the parameters. The parameter errors will only be slightly larger than those from a D-optimal design. The I-optimal designs do not guarantee orthogonality either as that is not part of the optimization criteria.
So all of this means that the user should choose the optimality that best meets their needs. There is no such thing as "the best" design. The "best" design will depend on the researcher's objectives and wants/needs from the design. Those are determined by people, not statistics. Therefore, different opinions can lead to different designs and design approaches. After all, someone could say that you should have only created one design and not augmented the original design. I don't believe that, but I hope you see the point. The design creation process utilizes the science knowledge of the experimenter as much or more than it utilizes the statistical/mathematical properties of a design.
So is the approach that you outline of a D-Optimal augmented with I-optimal a valid approach? Absolutely. Is it the best? That will depend on YOUR needs. I can tell you that it is a fine approach and you should get a design with good mathematical properties. The resulting design would not have as good of a D-optimality criteria as if you had created the entire design using D-optimality. The resulting design would likely not have as good of an I-optimality criteria as if you had created the entire design using I-optimality. But that is okay, as long as the design meets your purposes and allows you to build a good model that answers your questions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Augmented design with diffrent optimality criteria
Mr. Dan,
I really appriciate for your detail explanation.
I want to state that i suspect model needs 3rd order power because of the fluctuations in the plot of std residuals vs predicted values. What do you think about it, is it a sufficient clue to include third order power to the model?
Beside this, your explanation about I and D optimal designs is very clear but i still do not understand some points. This may be because of my lack of thoretical knowledge but i want to learn.
You said below that "I-Optimal designs are best at predicting."
One needs best model estimation for best predictions. That means that we need a best design at estimating parameters which is D-Optimal designs. So, i am little bit confused that which optimality criteria should be used for the study which aims to construct a good models and then make optimization by using profiler to find the best factor levels for targeted response values.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Augmented design with diffrent optimality criteria
I am glad that my explanation helped some.
When it comes to the cubic term, what does a plot of the raw data versus the factors look like? Knowing the science behind your data, does it make sense that you would see a cubic relationship? It looks like you have one point that was not predicted well when the prediction of stress was near 1700. Have you verified that the data is real and not an outlier? Cubic terms do not appear that often, so people often question when they do appear. But it very well could be real, and based on your residual plot, I understand why you added a cubic term.
As for the D and I-optimality stuff, it is easy to think that the most precise parameter estimates (D-optimal) will naturally lead to the lowest prediction error (I-optimal), but that is not necessarily the case. Consider the case of only one predictor variable, X, and a total of 9 runs. If I want a quadratic model, we will need to study 3 levels of X. If I want the best possible parameter estimates, I would put 3 runs at the lowest setting for X, 3 runs at the middle setting, and 3 runs at the highest setting. I need to put more runs at the extremes to better model that linear term. This is what a D-optimal design does.
What about for prediction error? Well, prediction error is "minimized" somewhere between the low and mid settings and again somewhere between the mid and high settings:
How could I get rid of the hump in the middle? Move some points from the ends to the middle. This is what the I-optimal design does. It uses two points at the ends of the X-range and places 5 points in the center. This will lower the prediction variance in the center, but the ends will be raised.
Remember, I-optimal is for integrated variance, so the "area under the curve" is minimized this way. This is why when people are trying to optimize a process, they want the optimum to be somewhere near the middle of the design space because an I-optimal design provides the best predictions in that area.
If you like mathematics and matrix algebra, remember that your model is:
D-optimal designs work on minimizing Var(B-hat).
The I-optimal designs focus on the left-side of that equation. Specifically,
and minimize the integrated variance of Y-hat. Notice that the variance in this formula is for a specific point of your inputs (X sub-0). The variance is calculated over the entire design space and integrated for I-optimal designs.
I hope this helps.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us