Any suggestion for DoE on chamber matching?

[#1]

Hi,

I have some questions about designing an effective DoE for chamber matching.

Suppose that we have four identical chambers that share global factors "A" & "B", whereas Factor "C(n)" can be applied to each chamber.

In other words, factors "A" & "B" will be applied to all four chambers at a time.

Suppose that all Factors A&B&C have some 2nd order interactions, whilst dominant estimates come from Main effect of each factor to responses.

We have outputs "X(n)" & "Y(n)" for each chambers(=n), but residuals to mean regression line for all four chambers has to go minimum = chamber matching.

Suppose that the regressions for Factors to Responses are generally linear, how can we make this DoE efficient?

[#2]

Okay, this sounds quite complicated so let me confirm a few things.

• For each run of the experiment you get a value of X and a value of Y for each chamber: X1, Y1, X2, Y2, X3, Y3, X4, Y4.
• And for each run you would plot X vs Y and fit a basic linear model.
• You would then look at the residuals from this model.
• If the residuals = 0, i.e. RMSE = 0, then the chambers are matched.

Is that all correct?

Is finding settings that minimise the residuals the objective of this experiment?

Also, you say that factor C can be applied separately for each chamber.

So does that mean that you have 4 factors (C1, C2, C3, C4) that can be set entirely independently of each other?

Thanks,

Phil

[#3]

Hi, thanks for your help!
All of your dotted statements are well established and correct.

Is finding settings that minimise the residuals the objective of this experiment? - Yes
So does that mean that you have 4 factors (C1, C2, C3, C4) that can be set entirely independently of each other? - yes totally independent to each other.

So this is tricky part that C1/2/3/4 are not correlated to each other whilst A&B are global factors.
C1/2/3/4 can be the fine tuning knob to minimize the residuals, whereas A&B are to make big shift to X&Y.

Thank you!

[#4]

Hi @Phil_Kay 

Since you have mentioned that you need to think about the way to solve this to build up DoE, will you be able to answer my main thread?

Thanks,

Joel

[#5]

Sorry for not replying sooner.

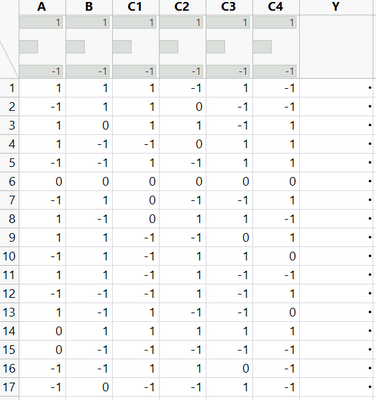
If all factors can vary independently, would this experiment (data table attached) be possible:

where -1 is the lowest setting of the factor, 1 is the highest setting, and 0 is the centre of the range.

This is a definitive screening design.

If you are able to carry out all the runs you could then find which factors are most influential in determining the RMSE of Y vs X.

I would also encourage you to search the internet for "design of experiment" and "chamber matching". There appear to be some published articles about this that you would probably understand better than I can. (I have not worked in the semiconductor industry)

You might also want to think about functional data explorer in JMP Pro because this enables you to model how a functional response varies due to the factors in a designed experiment. You could model how your Y vs X changes with the factors A, B and C1 to C4. This primer might help.

Let me know if this helps,

Phil  

Let me know if this helps.

[#6]

Sorry, a little late to the discussion and perhaps I don't understand the situation, but it doesn't sound like you are screening (only 3 variables) so DSD would not be what I would use.  Here are my thoughts, again it is very difficult to provide great assistance as the complete context is not provided:

1. First, the way I read the situation is you have a factor C that can be set for each chamber (this could be considered nested in chamber?) and Factors A&B that are factorial?  But then you also suggest you want the interactions with C?

2. You could think of chambers as "Blocks" or replicates (but treat as a fixed effect).  Essentially running the same factorial for each chamber.  A, B & C design simple 2^3, so 32 treatments.  This gives full resolution for all main effects, 2nd order and 3rd order interactions as well as chamber effect and chamber-by-factor interactions. The chamber-by-factor interactions could be useful as what matching chambers would also mean is the absence of chamber by factor interactions (the effects of the factors are consistent over chambers). You might be most interested in the C-by-Chamber interaction.

3.  Or you could try a more sequential approach, Run the 2^3 factorial on one chamber, then perhaps replicate on one other and compare...what did you learn.  Then you could modify your design and then decide what to run on the remaining chambers.  Or run the 2^2 factorial over all chambers and then experiment on C separately for each chamber.

4.  There is no mention of whether you predict non-linear polynomials...so perhaps understand the linear effects before adding quadratic effects?