- Due to inclement weather, JMP support response times may be slower than usual during the week of January 26.
To submit a request for support, please send email to support@jmp.com.
We appreciate your patience at this time. - Register to see how to import and prepare Excel data on Jan. 30 from 2 to 3 p.m. ET.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Adjusting y axis labels when plotting box-cox transformed data
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Adjusting y axis labels when plotting box-cox transformed data
JMP® Pro 16.2.0When plotting box-cox transformed data - how can the y axis value label be set to show the original scale? In log transfomation one can simply select a linear scale and the actual value scale is shown but with log spacings. There does not seem to be any simple way of doing this in y-axis settings. JMP® Pro 16.2.0
- Tags:
- macOS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Adjusting y axis labels when plotting box-cox transformed data
Maybe post an example of what you're trying to do?
A little more detail might be helpful.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Adjusting y axis labels when plotting box-cox transformed data
Thanks Byron. For most of my data, that raw regression does not fit the model and having soughte statistical advice, box-cox transformation sorts this out. However, the scales are not the same.
This is a screenshot of the raw regression
and here a screenshot of the box-cox transformed regression
its clear that the y-axis tick labels are directly based on the transformed data which no surprise. But there seems to be no way to simply instruct JMP to label the ticks with untransformed values. This is why I mentioned the matter of when doing log transformed plots one can select to show the non-transformed values and what happens is the ticks then move to the classic visualisation of a log scale, rather than being equally far appart but labelled with log values.
So my question is around tick labelling not aorund using box-cox transform.
These graphs, with a little tweaking are perfectly publication quality without me having to spend hours messing aroubnd with the very clunky and unintuitive graph builder.
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Adjusting y axis labels when plotting box-cox transformed data
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Adjusting y axis labels when plotting box-cox transformed data
I think I understand what you want to do. It seems entirely reasonable, and also not so easy. I will at a minimum try and articulate in more detail what you want, with a specific example.
Step 1.
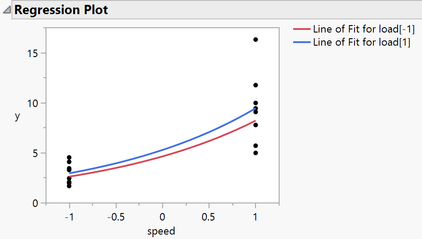
I have my model, which for the special case of a single continuous variable, or one continuous and one discrete (as here) is shown in the Regression Plot outline.
In this example its reasonable apparent that variance increases with speed and this can be improved with a Log transformation to the response. This is confirmed by evaluating Box Cox transformations ( λ = - 0 is equivalent to a log transform).
For convenience of illustration I will take the log transform rather than λ = -0.025.
Step 2
From the Box Cox transformation red triangle I can refit with a transform and specify the λ value.
The new model looks like this:
It is linear with respect to the transformed response. It is clearer to understand the model by looking at the profiler, which shows the y-axis in the un-transformed units:
What I believe @Grumpybaldprof is asking for is the profiler curve on the regression plot. I can make this more explicit:
Step 3
This time I return to the Fit Model platform and specify a Log transformation to the response variable.
Now I get the following Regression Plot :
This I think is what @Grumpybaldprof is looking for.
However, I'm only able to achieve this by applying the transformation in the Fit Model dialog and I am limited to the following power transformations:
These correspond to λ values of 0 ,0.5 ,2 , -1 respectively whereas the Box Cox transformation produces a continuum of values.
So what to do:
- Ask JMP to support the box-cox λ parameter when transforming the response, so that the reverse transformation is automatically applied to graphs
- Take a sensible interpretation of the Box-Cox transformation (99% of the time I end up taking a log transformation; I would never use λ=-0.025 because I don't know what it means)
- Use graph builder to recreate the graph
Step 4
Using graph builder - well it's not the easiest thing to do, let alone describe so I will just give a screenshot to show it can be done
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Adjusting y axis labels when plotting box-cox transformed data
Thanks David
That is very helpful and moves me forwards a bit. I will ask JMP as you suggest - would it be best to use the JMP Wishlist or is there better way?
It has also struck me that it might be quicker, meanwhile, to manually relable the axes - but I am certainly not clear on how to get the reverse values out of JMP. Any suggestions?
Cheers
Paul
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us