ANN and FDOE comparison

[#1]

Hello everyone,

I need help understanding the best approach to apply to my data.

I constructed a dataset with 84 batches from various experimental designs (DoEs) in the development of a pharmaceutical drug product. After that, I built an ANN model to predict drug release. Now, I would like to predict drug release (functional response) using JMP Pro Functional DOE (FDOE) and compare with the findings to the ANN model’s.

1. Does this comparison make sense? What is the best statistical method for comparing these two procedures (ANN and FDOE)?
2. How can I choose the number of knots in the FDOE platform?
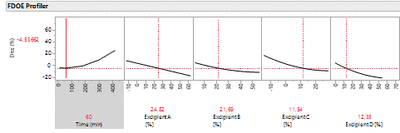
3. In the FDOE Profiler (see picture) several formulation parameters resulted in negative drug release.  What does this mean? for some formulation parameters I obtained a negative value of drug release. Is this to imply that this FDOE approach may not be predictive of the first time points in my dissolution profile?

 

I have already seen the Discovery Summit presentation (https://community.jmp.com/t5/Discovery-Summit-Americas-2021/A-New-Resolve-to-Dissolve-Model-Drug-Dis...), but are there any additional resources or literature I may read?

I am sorry if I am not making myself clear.

Thank you so much for your help!

[#2]

Please confirm that your response data are functions, perhaps a curve showing the progress over time of drug release for a batch.

Yes, it makes sense to compare myriad candidate models. You can use Analyze > Predictive Modeling > Model Comparison for this purpose.

Have you studied model selection in general or the FDE information regarding the number of knots?

The FDOE approach is based on linear regression. Regression assumes that the response varies between negative infinity and positive infinity. Your model might exhibit a lack of fit or bias near the limits of the response. You can use the FPCAs as the response with nonlinear models or any other model in JMP.

[#3]

Hi @sofiasousa24,

I will try my best to answer your different questions based on the limited context and data available. Please ignore any information or answer that could be irrelevant to your topic.

1. Yes and No, no strong opinion on this question.
   No: On a data point of view, your data are not independant, so using a Machine Learning model to predict all drug releases responses at different time points independently from each other does not take into account the time dependency of the response (and redundancy of the information), and the correlation of the response measured at different time points. 
   Yes: Machine Learning has fewer assumptions in model building than "classical" statistical modeling. Moreover, neural networks can be used for time series analysis and forecasting, since they can approximate nonlinear functions and may be more robust to multicollinearity than traditional modeling methods.
   For comparing these two procedures, you have to set similar conditions for training, validation and testing : make sure to use the same samples for training, for validation and testing, either with a cross-validation approach and the use of a validation column, or split your dataset and separate your test set from the rest of the data to avoid data leakage and use K-fold cross-validation with the same seed. If the algorithms have been trained and validated on the same data, comparing them on the same test data will be much easier.
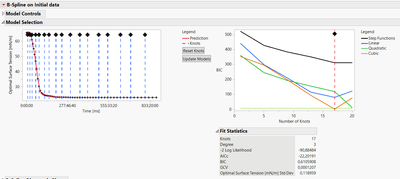
   You can start simple for the comparison of the methods, by plotting predictions vs. measured values, to see if you are able to predict the same trend as in your original data. Visualizing the distribution of the residuals may also help, to see what are the maximum errors and how they are distributed for each method. You can also plot residuals vs. predicted, to see if the errors remain stable regarding increasing values, or if you encounter heteroscedasticity (the variance of the prediction increase with the values of X/time). Finally, you can also calculate an aggregated metric of performance for both methods, like RMSE/MSE or any other metric related to the residuals (difference between predicted value and measured value). Aggregated values helps simplifying the comparison, but they may "hide" some details you may have seen through visualizations as explained before.
   
   
2. In the FDOE platform, the number of knots is recommended by default when doing the analysis : 
   

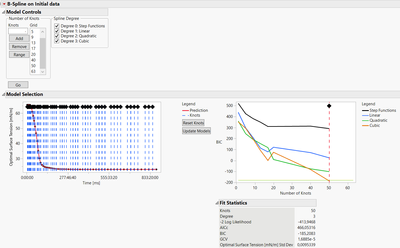
   When launching a type of model (B-Splines, P-Splines, Wavelets, ...) JMP will try a number of different knots size (which can be seen in the panel "Model Controls"). By default, JMP will choose a number of knots (and the degree of functions for Splines)  that minimize BIC (Bayesian Information Criterion), which is an information criterion that balances the predictive performance of the model with its complexity : the lower the better. Very often the range used by JMP will be sufficient to find a local minimum, but you can try to extend the range of knots number in the Model Controls to see if you're able to achieve a lower BIC :

   

   However, if you're increasing the number of knots closely to the number of (time) measurements for each batch of your datatable (like in the example above), make sure to use a validation set to avoid creating an overfitted model that works perfectly on this training set but performs poorly on other external data.

3.  There may be a lot of things to check in the FDOE platform before commenting on the results of the model :
   - Which model did you use and why (B,P-Splines, Wavelets, ... ?) ? Have you used any preprocessing steps for your data ?
   - How much knots and which degree of the functions did you use ?
   - Did you use a validation set ?
   - What is the variability and reproducibility of your measurement process ? Are the errors of the FDOE too big compared to measurement variability ?
   + Questions about the NN : how it has been built, with how many layers, which activation functions, which validation, etc... The Neural Network Tuning may be helpful to design an efficient and appropriate neural network structure for a specific problem. However, Neural Nteworks are usually the last model I tried if others (more simple) models have failed, due to their complexity and lack of interpretability.
   
   Also take into considerations that FDOE enables you to fit directly a regression model to the principal functional coefficients in the platforms, but you can also extract the coefficients of the curves and do manually the modelling with all other modelling platforms from JMP, to access more flexible Machine Learning algorithms that require less assumptions.

I hope these first points will provide you an overview and a fresh start in the discussion,