JMPでは、[グラフ] メニューに「三角図」というグラフを作成できるプラットフォームがあります。3つの成分をもつデータをグラフ化し、分布やばらつきを調べるのに有用なグラフではありますが、実験計画法における配合実験で用いると効果的なケースがあります。
「三角図」では、以下に示したようなグラフを描くことができます。グラフ上の色のグラデーションは、実験計画法で作成したモデルの予測値を等高線として示したものです。
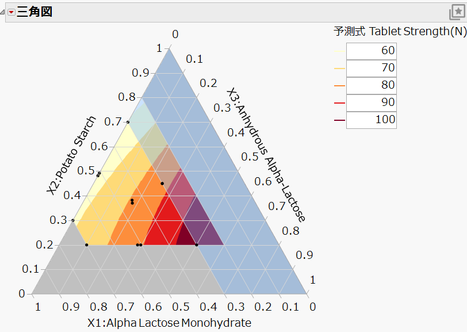
このような図は、どのような手順で描くのでしょうか。配合実験の具体例を示しながら説明します。
配合実験とは
配合実験とは、配合物の成分(比率)を因子とする実験のことであり、各因子の取りうる値が0(0%)~1(100%)の範囲にあります。さらに、すべての因子の比率の合計は1(100%)という制約もあります。このため、実験空間は(因子数 - 1)次元の領域となります。
例えば、3つの配合因子 X1, X2, X3があったとき、X1+X2+X3 = 1 という制約があるため、実験空間は3次元の立方体から三角形の平面を切り出した2次元の領域となります。

配合実験の例
医薬品開発における錠剤設計で、以下の3つの賦形剤(ふけいざい、固形製剤に加える添加物)と錠剤の硬度との関係を調べたいとします。
| 賦形剤 |
配合できる割合の下限と上限 |
| X1:Alpha Lactose Monohydrate(α-ラクトース一水和物) |
20%~70% |
| X2:Potato Starch(ジャガイモのでんぷん) |
20%~80% |
| X3: Anhydrous Alpha-Lactose(無水α-ラクトース) |
0%~60% |
さらに、物性上の観点からX2 とX3を合計して70%以内に収めることにします。
三角図で実験点を視覚化
JMPの「カスタム計画」を用いて、上記の配合因子の条件を設定します。この例では、配合因子の主効果と2次の交互作用を含めたモデルとし、実験回数は12回とします。

作成された配合実験の計画を「三角図」プラットフォームを使って視覚化します。三角図の灰色の領域は各因子の取りうる値の範囲外であり、水色の領域はX2 + X3 ≦ 0.7 を満たさない領域です。すなわち、三角図の中で白色の領域が、この例での実験空間となります。

実験空間内に黒い点がプロットされていますが、これが実験点です。白色の領域の頂点や辺、領域中心付近が実験点がプロットされています。
カスタム計画で得られた実験点に基づき、賦形剤の割合を調整して製造したときの錠剤の硬度(N)を測定し、テーブルのY(応答)のセルに入力します。
実験が終了したら、「モデルのあてはめ」プラットフォームを用いて配合モデルをあてはめます。「モデルのあてはめ」では、[配合プロファイル]というオプションがあり、ここでも三角図に相当するものを描くことができます。

ここで予測値の等高線を描いたり、配合割合を変化させたときの錠剤硬度の予測値を探索できますが、等高線の値に応じて色のグラデーションをつけることはできません。
学術論文などでは、等高線にグラデーションをつけて表示する例がよく見られるため、その方法を行うには、最初に示したようにグラフメニューにある「三角図」のプラットフォームを利用することになります。
予測式を反映させた三角図
「三角図」では予測式の等高線を図の中に含めることができ、等高線にグラデーションをつけることができます。具体的な操作方法は以下の通りです。
等高線を含む三角図の作成(操作)
- 「モデルのあてはめ」のレポート左上にある赤い三角ボタンから [列の保存] > [予測式] を選択します。すると、データテーブルに予測式を含む列が保存されます。
- [グラフ] > [三角図] を選択し、[X, プロット] に配合因子の列(3つ)を、[等高線の計算式] に保存した予測式を含む列を指定します。
- レポート「三角図」の左上にある赤い三角ボタンから [等高線間を塗りつぶす] > [上を塗りつぶす] を選択します。
- 必要に応じて、オプション [カラーテーマ]で等高線のカラーテーマの指定、右上の凡例にある数値を変更し、等高線の閾値を変更します。

これらの操作で、三角図にグラデーションをつけた等高線を含めることができました。錠剤硬度を高めたい場合は、濃い色の領域の配合割合を検討することになります。例えば、実験領域の右下である X1: 30%, X2: 20%, X3:50% は、錠剤硬度の予測値が最も大きくなる点なので、これらの配合割合で錠剤を作成し、硬度を測定し、大きな硬度が再現できるか確かめる方法が考えられます。

このように配合実験による求められる応答と配合因子の関係式を等高線としてあらわす際、等高線を色のグラデーションで表示すると理解しやすくなります。そのため、JMPでは「三角図」で等高線のグラデーション表示できることを知っておくと良いでしょう。
by 増川 直裕(JMP Japan)
Naohiro Masukawa - JMP User Community