「ムーアの法則」は今後も成立するのかどうか？ JMPとChatGPTで考察してみた

[#1]

最近のChatGPT（GPT-4）では、画像をアップロードすることによりその画像を認識できるようになっています。

そこで何気なく、以下のようなJMPのレポートを画像形式（png）にしたものをChatGPTにアップロードし、「これはJMPで曲線をあてはめたときのレポートですが、この結果を解釈してください。」というプロンプトを試してみました。

すると、次のような文書を返してくれました。

この後、この画像にあるAICcやBIC、R2乗の値を認識して結果を解釈していましたが、何よりも驚いたのは最後に記述された以下の文章です。

おー、特に説明していないのに、このデータが「ムーアの法則」を示すものだと認識しているではありませんか！！

ChatGPT恐るべしです。

「ムーアの法則」とそれを示すグラフ

ムーアの法則とは、集積回路あたりに搭載されるトランジスタの数が、およそ2年ごとに2倍になるという法則です。半導体技術は日々進歩しており、搭載されるトランジスタの数が多くなるほど機器の処理能力は大幅に向上するので、私たちの生活でもその恩恵を多大に受けています。

ムーアの法則を説明するときに、次のようなグラフが良く用いられます。

年を横軸（X）に、その年における「マイクロプロセッサーあたりのトランジスタの数」を対数変換したものを縦軸（Y）としてプロットし、回帰直線をあてはめたものです。ここでは、2年で2倍になることがわかりやすいように、底が2である対数を使って変換しています。

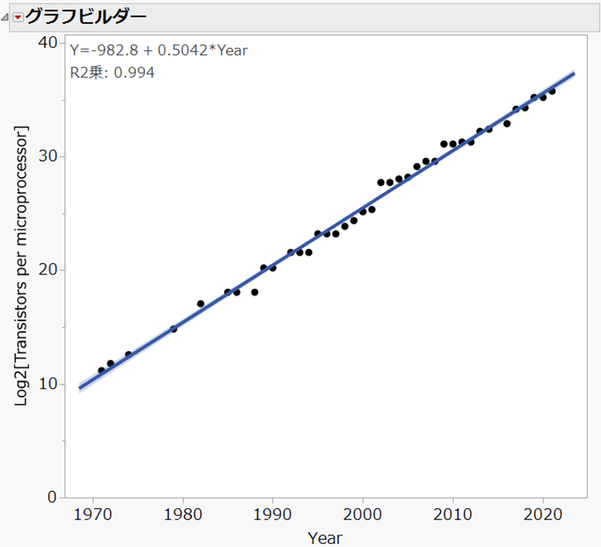
R2乗は0.994ととても高く、回帰直線がデータによくフィットしています。回帰式は1年ごとに対数変換されたトランジスタの数は約0.5増加していることを示していますので、2年では約1増加することになります。これを元のスケールに戻すと、2年ごとにトランジスタの数は約2倍になる、すなわちムーアの法則そのものを示しています。

JMPの「曲線のあてはめ」でさまざまな非線形モデルをあてはめる

前節ではトランジスタの数（Y）を対数変換したものが直線に従うことを示していますが、元のスケールで考えるとYは指数関数的に増加していることを示しています。

そこで、Yを対数変換せずにそのままのスケールで非線形モデルをあてはめた結果が、本ブログの最初に示したレポートなのです。

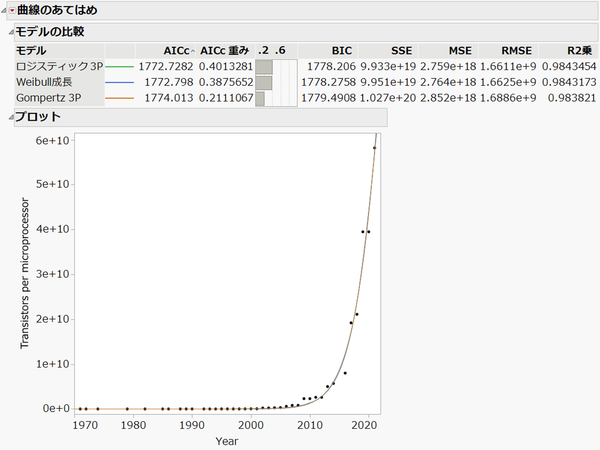
JMPの [曲線のあてはめ]　プラットフォームでさまざまな非線形モデルをあてはめていますので、もう一度このレポートを参照してみましょう。

ここでは、ロジスティック3P（3つのパラメータを持つロジスティックモデル）、Weibull成長（成長曲線）、Gompertz3P（3つのパラメータを持つゴンペルツ曲線）の3つのモデルをあてはめています。

グラフ上のあてはめ線をみると1つしかあてはめていないようにも見えますが、3つのモデルともほぼ同じあてはめなので重なっているのです。

レポート上側にある「モデルの比較」レポートでは、それぞれのモデルのあてはまりをAICc、BIC、R2乗などの統計量で比較できます。JMPの仕様としてAICcが小さい（あてはまりが良い）順に上から下へと並べられているので、ロジスティック3Pが一番良いモデルとはなりますが、他のモデルの統計量も類似しており、モデルの優劣をつけるのは難しいようです。

今後もムーアの法則は成り立つのか？

前節では1971年から2021年のデータを用いて非線形モデルをあてはめましたが、これらのモデルを使って今後のトランジスタ数を予測した場合はどうなるでしょうか？

実は、モデルによって予測が大きく異なってくるのです。以下は、先ほどのグラフの横軸を2040年ごろまで広げたものです。

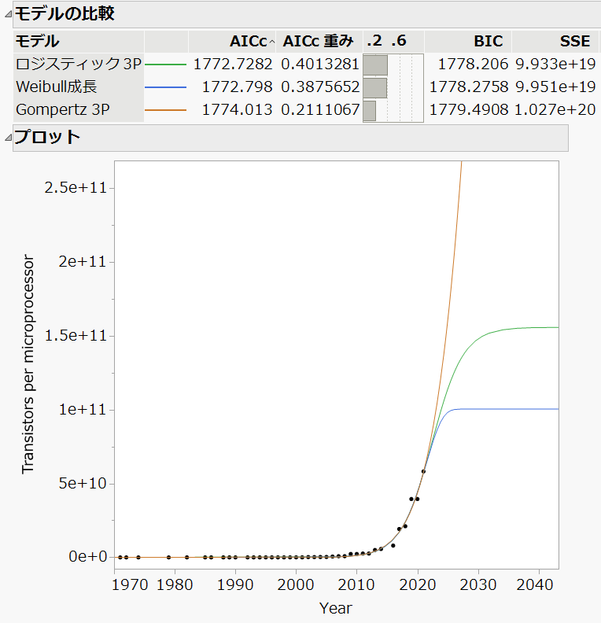
オレンジ色のGomperz 3Pモデルは、今後もずっとムーアの法則が続いていくことを仮定した予測です。一方、ロジスティック3Pモデル、Weibull成長モデルは途中でムーアの法則が破綻し、トランジスタ数の伸びが鈍化することを仮定した予測です。

確かに、近年ではムーアの法則は限界にきていると言われています。それなら、ChatGPTにムーアの法則の今後について聞いてみましょう。

ある程度限界が来ていることは確かなようです。物理的、経済的な要因が今後、ムーアの法則を維持できるかのキーになりそうですね。

ムーアの法則が現在でもあてはまっていることは、技術者がその法則に従うように技術革新を行ってきた努力の結果なのかもしれません。今後も、ムーアの法則が継続されていくような技術革新を期待し、私たちの生活をより良いものにしていくことを勝手ながら期待してしまいます。

by  増川 直裕（JMP Japan）

Naohiro Masukawa - JMP User Community

データの出典：Our World in Data (Moore's law: The number of transistors per microprocessor (ourworldindata.org))