「カテゴリカル」を利用したアンケート分析 Part 2: 集計から分析へ！ ～属性間で回答分布を統計的に比較する～

[#1]

前回のPart 1では、「カテゴリカル」プラットフォームを用い、アンケートデータがもつさまざまな形式の回答（単一回答、複数回答、スコア）を一度に集計する例を示しました。

とはいっても、集計のレベルであれば頑張って表計算ソフトでもできますし、アンケートシステムを利用しているのであればシステム上で集計結果を表やグラフで表示してくれます。

では、JMPの「カテゴリカル」を利用するメリットは何なのか？

それは、今回紹介するグループ間で回答分布を比較できることなのです。

「カテゴリカル」でグループ変数を指定

アンケートの分析では個々の回答を集計するほかに、回答者の属性（性別、年代など）で分けて回答の集計が行われます。いわゆるクロス集計と呼ばれるものです。

Part 1で扱ったSQCの研修の例で考えてみましょう。この例では「役職」（一般、役職あり）という属性があるので、役職別に他の回答について集計し比較してみます。

上のデータテーブルについて、次の分析を行ってみます。

 

役職　×　受講のきっかけ（複数回答）：多重応答

役職　×　統計ソフトの使用経験（単一回答）：　名義尺度

役職　×　時間配分、テキストの構成、実用性（スコア）：順序尺度

役職　×　満足度（スコア）：順序尺度

このとき「カテゴリカル」において、以下のように「役職」を [X, グループ化カテゴリ]　に指定します。

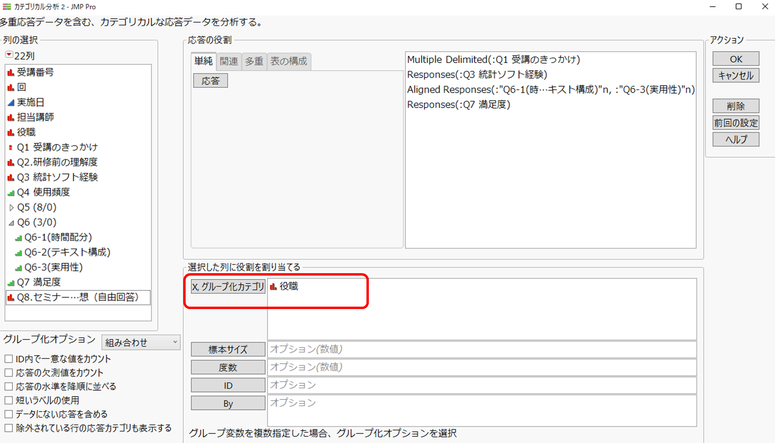
割合の等質性検定（グループ間で回答割合が異なるか？）

最初に、多重応答である"受講のきっかけ"と名義尺度である"統計ソフト経験"（あり/なし）について、レポートを参照してみます。以下のように、"一般"と"役職あり" で分けて集計されたクロス集計表が表示され、対応するシェアチャートも表示されています。

 

"受講のきっかけ" を、一般と役職ありで回答のシェアを比較してみると、以下の項目でシェアの差がありそうです。

上司の指示：　一般（24.7%）、役職あり（16.8%）

SQCへの興味：一般（8.9%）、役職あり（16.1%）

統計ソフトの経験についても、一般の経験者は39.6%、役職ありの経験者は50.9%とこちらも差がありそうです。

ここで記載したのは、あくまでも"差がありそう"ということです。統計ソフトを使っているので、統計的に差があるかどうかを調べたいですね。そこで「カテゴリカル」にある検定のオプションを用います。

多重応答でない応答の等質性検定

統計ソフトの経験のように多重応答でない回答の場合、[応答の等質性に対する検定] オプションを実行します。

グループ間で応答の等質性が検定されるのですが、ここでは、役職間で応答の割合が等しいという仮説に対する検定を行っています。クロス集計表の独立性を調べる目的で使われるカイ2乗検定に相当します。

レポートの尤度比カイ2乗、Pearsonのカイ2乗に対するp値は0.05より小さいので、検定の有意水準を5%とすると、応答は等質でない、すなわち役職間で統計ソフト経験の割合に差があることを示しています。

多重応答の等質性検定

複数回答である "受講のきっかけ"  には、[多重応答の検定]　を用います。ここでは、応答のカテゴリに対して選択/非選択の二項分布を仮定した [二項分布の等質性検定] のレポートを示します。

レポート「各応答に対する二項検定」では、各設問の回答割合をグループ間で比較した統計量が表示されます。

例えば"上司の指示"の応答に対し、全体数と回答者は以下のようになります。

一般では392人中144人が該当　（ 36.7% = 144/392）

役職ありでは111人中26人が該当　（ 23.4% = 26/111）

このとき、応答割合をY（二項分布を仮定）、一般/役職ありをXとしたロジスティックモデルによりカイ2乗値やp値（=0.0074）を求めます。

レポート「各応答に関する二項検定」を参照すると、"上司の指示"、"SQCへの興味"　の2項目について有意差が認められます。これより、一般社員は上司に受講しろと言われたからセミナーを受講した、役職がある人はSQCそのものに興味があるといったことが示唆されます。

他の項目は、一般と役職ありで割合に差があれど、有意な差ではないようです。

スコアを比較

商品の満足度などを問う設問では、5段階評価などのスコアで回答することが多いです。その際、グループ間でスコアに差があるかどうかを確認したいでしょう。

今回の例では、セミナーの時間配分、テキストの構成、実用性を5段階評価、セミナーの満足度を10段階評価で回答してもらっています。役職間でこれらの評価スコアの比較をするのであれば、下記のように [スコア平均の比較] を用いてみます。

セミナーの時間配分、テキストの構成、実用性についてのレポートです。クロス集計表の右側に応答1～5をスコアとみなしたときの平均、標準偏差が表示されています。

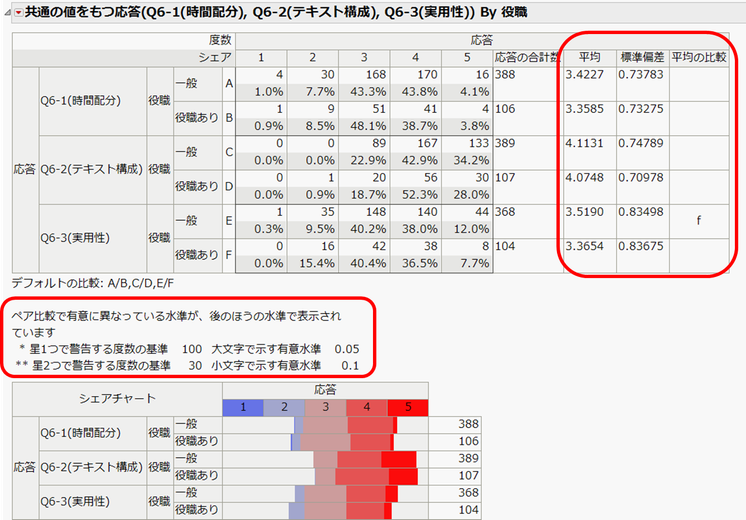
最後の列「平均の比較」を参照すると、5行目（一般の実用性に対するスコア、Eと表示）に "f" の文字が表示されています。これは、Fと表示されている6行目（役職ありの実用性に対するスコア）に対して有意水準0.1で有意であることを示しています。（図中の赤枠で囲んだ説明をご参照ください。）

実用性について一般のスコア平均は3.52、役職ありは3.37であるが、これらの平均をペア比較した際、検定（t検定を使用）のp値が0.1より小さかったことを示しています。役職ありの方は一般に比べて、セミナーの実用性については少し不満だったのかもしれません。

セミナーの"満足度" に関するレポートも参照してみましょう。

一般の平均が7.23、役職ありの平均が6.91であり、「平均の比較」の欄には"B" の文字が表示されています。大文字で示されているので、この場合は有意水準0.05で有意であることを示しています。セミナー自体の満足度につきまして、一般と役職ありではスコアに有意な差がありました。

多くの設問に対するグループ間比較に有効

「カテゴリカル」では、グループ化変数を指定することにより、グループ別の集計、比較が行えます。実際アンケートでは多くの設問、多くの回答選択肢が存在する場合があります。そのようなとき、たくさんの表やグラフが表示されるので、結局どの回答に差があるかを一つずつ調べていくのは大変です。

今回説明した「応答の等質性の検定」、「スコア平均の比較」を使うと、差のある項目が一目でわかるので、効率的にグループ間の回答比較ができます。

次回のPart 3では、アンケートの複数回答形式の設問を扱う「多重応答」について詳しく解説します。