Use to interactively explore the relationships between Power, Sample Size, and Alternative Proportions in testing a hypothesis for a single population proportion. See the Hypothesis Tests and Confidence Intervals for Proportions guide to learn how to test a hypothesis for a population proportion.
Sample Size and Power - One Sample Proportion
- Select DOE > Sample Size Explorers and choose Power > Power for One Sample Proportion.
- Choose the type of test: One-Sided or Two-Sided and Alpha (significance level for the test).
- Choose Method (Exact Test or Normal Approximation).
- Enter the Assumed Proportion. This is the value of the population proportion being tested and assumed under H0. Here we are planning on testing the Hypothesis H0: p = 0.50 vs. HA: p > 0.50.
- Enter the Alternative Proportion. This is the value for the population proportion under HA being considered. Here we consider the scenario of the population proportion being 0.75.
- Select parameter to solve for. Here we chose Sample Size.
- Enter a value for the Power. Here we entered 0.80.
The solution (n=23) is shown in the Sample Size field.
Note: The Power field changed to 80.77% since sample size can only be an integer.
n=22 results in a Power of 79.07%.
- Use the interactive cross-hair tool (or type in values) for Power, Sample Size, Assumed Proportion, and Alternative Proportion to study the relationship between these parameters solving for many different scenarios.
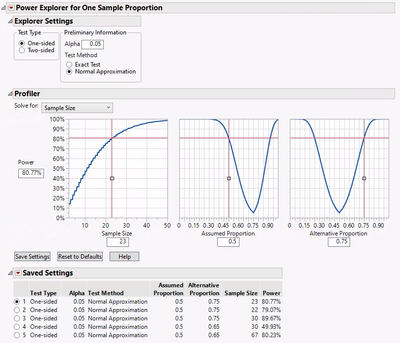
The settings and solution for each analysis performed can be saved. The table of saved settings shows the results of five different
analyses performed when testing the hypothesis H0: p = 0.50 vs. HA: p > 0.50
1. What sample size is needed to achieve a power of 80% assuming an alternative proportion of 0.75?
Answer: n = 23
2. What is the power with a sample size of 22 assuming an alternative proportion of 0.75?
Answer: Power = 79.1%
3. What is the power for a sample size of 30 assuming an alternative proportion of 0.75?
Answer: Power = 89.7%
4. What is the power for a sample size of 30 assuming an alternative proportion of 0.65?
Answer: Power = 49.9%
5. What sample size is needed to achieve a power of 80% assuming an alternative proportion of 0.65?
Answer: n = 67
Note: Determining sample size to achieve a desired margin of error in a Confidence Interval can be done using DOE > Sample Size Explorers > Confidence Intervals > Margin of Error for One Sample Proportion.
Visit Design of Experiments Guide > Sample Size Explorers in JMP Help to learn more.