Problem
I wanted to create this figure for a publication
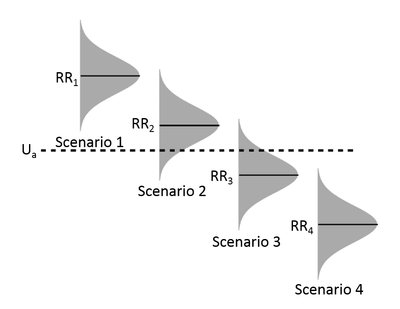
Solution
To create the vertically oriented shaded/filled and truncated normal curves, I utilized the Polygon() graphics function. The challenge was to easily and repeated be able to create that polygon that was scaled and located appropriately on a graph. I did this using this function
func_VNormalShape = Function( // create a polygon that looks like a vertically oriented normal distribution
{_xloc, _yloc, _xscale = 1, _yscale = 1},
{_VNormShapeX, _VNormShapeY},
// create a vector of y values to use for plotting the shape
_VNormShapeY = ((_yloc - 3 * _yscale) :: (_yloc + 3 * _yscale) :: (_yscale / 10))`;
// create the filled polygon boundary points
_VNormShapeX = V Concat(
J( 61, 1, _xloc ),
_xloc + Sqrt( 2 * Pi() ) * _yscale * _xscale * Normal Density(
Sort Descending( _VNormShapeY ),
_yloc,
_yscale
)
);
_VNormShapeY = V Concat(
_VNormShapeY,
Sort Descending( _VNormShapeY )
);
// substitute into the Polygon(function) the two vectors with the boundary point X and Y values
// and evaluate the function
Eval(
Substitute(
Expr(
Polygon( Expr( shape_x ), Expr( shape_y ) )
),
Expr( shape_x ), _VNormShapeX,
Expr( shape_y ), _VNormShapeY
)
);
);
the first two arguments of the function specify the "origin" or location of the distribution to be drawn (i.e. the (x,y) position for the center base of the distribution). The second two optional arguments are the scaling of the size of the distributions. The default size is based on a standard normal distribution, and the scaling is relative the x direction and y direction.
The result of the function is an evaluated expression that a graphics script used to draw the distribution as a polygon.
examples:
func_VNormalShape(1,3) creates the polygon statement for a vertically oriented standard normal distribution centered at x=1, y=3.
func_VNormalShape(2,4, 0.5, 1.5) creates the distribution centered at x=2, y=5, but the horizontal width is scaled down by a factor of 0.5 and the vertical width is scaled up by a factor of 1.5.
Discussion
Here is the full script that creates part of the of overall graphic. I saved the output from this script as an image file and then imported into powerpoint to add some annotations and arrived at the graphic shown at the top of the post
names default to here(1);
func_VNormalShape = Function( // create a polygon that looks like a vertically oriented normal distribution
{_xloc, _yloc, _xscale = 1, _yscale = 1},
{_VNormShapeX, _VNormShapeY},
// create a vector of y values to use for plotting the shape
_VNormShapeY = ((_yloc - 3 * _yscale) :: (_yloc + 3 * _yscale) :: (_yscale / 10))`;
// create the filled polygon boundary points
_VNormShapeX = V Concat(
J( 61, 1, _xloc ),
_xloc + Sqrt( 2 * Pi() ) * _yscale * _xscale * Normal Density(
Sort Descending( _VNormShapeY ),
_yloc,
_yscale
)
);
_VNormShapeY = V Concat(
_VNormShapeY,
Sort Descending( _VNormShapeY )
);
// substitute into the Polygon(function) the two vectors with the boundary point X and Y values
// and evaluate the function
Eval(
Substitute(
Expr(
Polygon( Expr( shape_x ), Expr( shape_y ) )
),
Expr( shape_x ), _VNormShapeX,
Expr( shape_y ), _VNormShapeY
)
);
);
_nw=new window("Figure",
_ob=Outline Box("Figure",
_gb=Graph Box(
suppressaxes,
x scale(0,5),
y scale(-1,11),
Xname(""),
Yname(""),
fill color("gray");
func_VNormalShape(1, 8, .75, .75);
line({1,8}, {1.75, 8});
func_VNormalShape(2, 6, .75, .75);
line({2,6}, {2.75, 6});
func_VNormalShape(3, 4, .75, .75);
line({3,4}, {3.75, 4});
func_VNormalShape(4, 2, .75, .75);
line({4,2}, {4.75, 2});
linestyle(1);
Pen Size(2);
line({0.5, 5}, {4.5, 5});
)
)
);
_gb[FrameBox(1)]<<{top(0), bottom(0), left(0), right(0)};
resulting output:
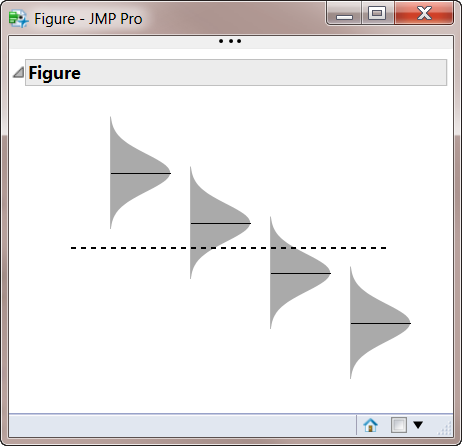
See Also
I wanted to share it again by itself, as it was really handy today when I pulled it out to make my figure.