- User Community
- :
- Blogs
- :
- JMPer Cable
- :
- Is it uniform?
조셉 지. 라미레즈 @ZenEos , 박사, WL 고어앤어소시에이츠
참고: 이 기사는 원래 JMPer Cable, 27호, Winter 2011에 실렸습니다.저자는 최근 Brenda Ramirez와 SAS Press Book을 공동 저술했습니다. Douglas Montgomery의 통계적 품질 관리 소개: JMP® 동반자 .
확률과 통계의 기본 과정을 수강했다면 아마도 균일 분포를 접했을 것입니다. 그것이 당신의 기억에서 가장 중요한 것이 아니라면 자신을 비난하지 마십시오. 균일 분포는 일정한 확률로 현상을 설명하기 때문에 그다지 매력적이지 않습니다. 주어진 간격의 모든 값에 대해 발생 확률이 일정한 공학 및 과학 분야의 응용 프로그램을 찾는 것은 어려운 것 같습니다. 이 간격의 숫자는 발생할 확률이 같아야 하므로 0과 1 사이의 의사 난수를 생각합니다. 균일 분포는 때때로 직선 도로를 따라 교통량 분포를 위한 모델로 사용되었습니다.
일반적으로 확률 분포는 데이터에서 관찰되는 불확실성의 정도를 설명하고 정량화하는 데 사용되는 수학적 모델 또는 방정식입니다. 연속 균일 확률 모델에서 값을 관찰할 가능성 엑스 구간 [θ,θ + σ ]는 일정하고 1/ σ 또는 1을 간격의 길이로 나눈 값입니다. 연속 균일(직사각형) 확률 밀도 함수를 설명하는 수학 방정식은 다음과 같습니다.
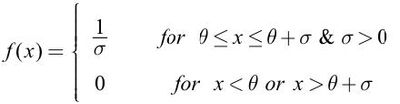
저희 블로그 독자 중 한 분, 통계 인사이트 , 균일 분포를 맞추는 방법을 물었습니다. JMP . Uniform은 Distribution 플랫폼의 Continuous Fit 상황에 맞는 메뉴에서 선택할 수 있는 항목 중 하나가 아닙니다. 그러나 베타는 선택 사항 중 하나입니다.
균일(θ,θ + σ) 베타 (1, 1, θ, σ).
다행스럽게도 JMP 선택 중 하나인 Beta 배포판과 Uniform 배포판 사이에는 편리한 관계가 있습니다. 베타 확률 밀도 함수의 일반적인 형태는 다음과 같습니다.
어디 비. ( α , β)는 베타 함수입니다. 이 PDF는 표준 2-모수 베타 분포를 일반화합니다. 베타 ( α , β) , 구간 [0,1]에서 임의의 경계 구간 [θ,θ]까지 + σ ]. 형상 매개변수 값이 다음과 같을 때 α = 1이고 β = 1이면 베타 함수 비. (1, 1) = 1이고 pdf의 일정한 확률은 1/ σ . 즉, X가 구간(θ,θ)에서 균일하게 분포한다면 + σ ), X는 임계값 θ 및 스케일을 갖는 Beta(1, 1)로 분포됩니다. σ .
이 관계를 살펴보자. 의 히스토그램 그림 1 구간 (0,1)의 균일 분포에서 100개의 시뮬레이션된 관측치를 보여줍니다. 이러한 관찰은 Formula Editor의 Random Uniform 생성기를 사용하여 생성되었습니다.
예상대로 이 분포는 다소 직사각형 모양입니다. 이 데이터에 균일 분포를 맞추려면 히스토그램 Uniform(0, 1) 제목 표시줄의 상황에 맞는 메뉴(빨간색 삼각형)에서 연속 맞춤 > 베타를 선택합니다.
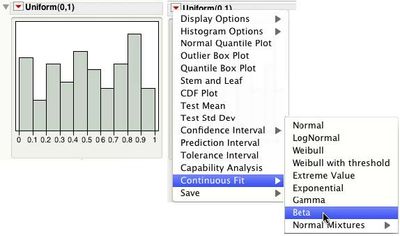
그림 2 직사각형 모양의 중첩된 베타 적합이 있는 히스토그램을 보여줍니다. 피팅된 베타 매개변수 추정값은 α=1.07 및 β=1.03을 보여줍니다(1에 가깝지만 얼마나 가깝습니까?). 에 대한 95% 신뢰 구간 α 그리고 β 둘 다 1을 포함하여 1과 다르다는 증거가 충분하지 않음을 나타냅니다. 실용적인 측면에서, 이는 α와 β가 1로 가정되므로 균일 분포가 이 데이터를 잘 설명함을 의미합니다. 임계값 매개변수 θ는 0.009이고 척도 매개변수 σ는 균일(0, 1)을 지원하는 0.977입니다. (θ와 σ 최대 가능성 추정치가 아닙니다. JMP는 θ를 최소 데이터 값으로 설정하고 σ를 데이터 범위(=최대-최소)로 설정합니다. 마지막으로 Diagnostic Plot은 95% 신뢰 범위 내에서 선 주위에 가깝게 맴도는 점을 보여줍니다.
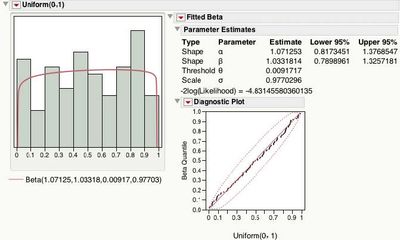
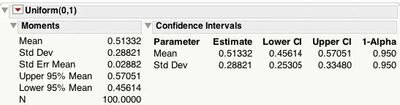
Uniform(θ, θ + σ)의 경우 평균은 θ + σ/2 이고 표준 편차는 σ/√12 입니다. 의 모멘트 테이블 그림 3 평균은 0.5에 가깝고 표준 편차는 1/√12 = 0.2886에 가깝습니다. 평균과 표준 편차에 대한 95% 신뢰 구간에는 각각 0.5와 0.2886이 포함됩니다.
Beta(1, 1, θ, σ))를 피팅할 때 찾아야 할 사항 균일 분포가 데이터에 대한 좋은 근사값인지 확인하기 위해 베타 분포 적합을 사용하려면 다음 단계를 따르십시오.
- 분포에서 베타 분포 적합 히스토그램 제목 표시줄의 빨간색 삼각형 메뉴에서 연속 적합 > 베타를 선택합니다.
- 모수 추정치 보고서를 보고 형상 모수 α 및 β에 대한 추정치가
- α 및 β에 대한 95% 신뢰 구간에 1이 포함되어 있는지 확인합니다.
- Fitted Beta 제목 표시줄의 빨간색 삼각형 메뉴에서 Diagnostic Plot을 선택합니다. 진단 플롯의 점은 직선에 가까워야 합니다.
- 유니폼( θ, θ + σ) 매개변수는 임계값으로 지정됩니다. θ 및 규모 σ.
- 히스토그램의 빨간색 삼각형 메뉴에서 신뢰 구간 > .95를 선택하여 평균 및 표준 편차에 대한 95% 신뢰 구간을 확인합니다(참조 그림 3 ).
- 확인 θ + σ /2(평균) 및 σ/√12 (Dev.)는 간격 내에 있습니다.
예: 브리즈번 베이비 붐 데이터 > 1997년 12월 18일은 호주 퀸즐랜드의 브리즈번에서 기록적인 날이었습니다. 44명의 아기가 Mater Mothers' Hospital에서 24시간 동안 태어났습니다.
그림 4 해당 날짜에 발생한 각 출생에 대해 자정 이후 경과된 시간(분)의 히스토그램을 보여줍니다. 24시간 동안 언제든지 출생이 발생할 수 있다고 믿는 것이 합리적이며 히스토그램이 이를 뒷받침하는 것 같습니다. 균일 분포가 데이터에 잘 맞습니까?
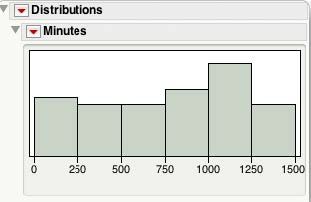
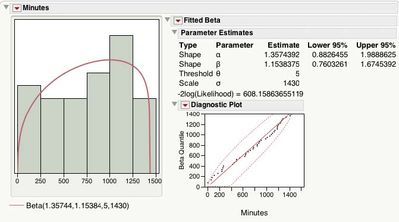
그림 6 평균 및 표준 편차에 대한 모멘트와 95% 신뢰 구간을 보여줍니다. Uniform(5, 1435)의 경우 평균은 5 + 1430/2 = 720에 가깝고 표준 편차는 1450/에 가깝습니다. √12 = 412.8054. 평균에 대한 95% 신뢰 구간에는 720이 포함되고 표준 편차에 대한 신뢰 구간에는 412.8054가 포함됩니다.
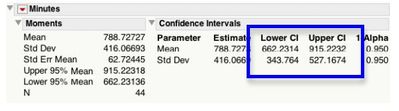
다음에 데이터를 균일 분포로 설명할 수 있는지 궁금하면 '베타'를 생각하고 연속 맞춤이 있는 분포 플랫폼을 사용하십시오. > 베타핏.
원래 Spanish 로 작성된 이 게시물은 귀하의 편의를 위해 번역되었습니다. 답장을 보내면 Spanish 로 다시 번역됩니다.
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Cookie Preferences
- Terms of Use
- Privacy Statement
- Contact Us

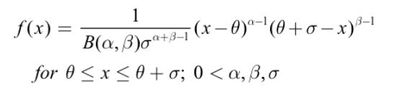
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.