Last month, we explored how to use latent variables in our path diagrams as well as how degrees of freedom can help guide us towards a functioning structural equation model. But how can we determine that a structural equation model not only works but also is a good model?
When we create a path diagram, it is up to us to determine which variables affect each other, and this is not a trivial task. When we construct a path diagram using our domain knowledge, it's possible that we get a model that works. But that doesn’t necessarily mean that the model we have created is a good model. Fortunately, there are a few metrics that we can use to determine quantitatively how good our model is. These are reported in the JMP Pro SEM platform for each model.

Quality of Fit Metrics
A few metrics are used in SEM to determine how good the fit of the model is. I won't go into detail on all the tests used, so if you would like a more in-depth rundown, I recommend the JMP help guide.
Instead, I would like to go over a couple of the fit indices that I use and have found to be the most useful when determining the “best” model. The first of these is the AICc. A lower AICc value means a better-fitting model. I prefer this metric because it takes into account the size of the model but doesn’t put too much emphasis on it. In my experience, BIC focuses too much on smaller models and so favors these too much. The other benefit of using the AICc is that JMP Pro gives a weighted AICc, which shows the probability that the model being studied is the correct model compared to the other models.
While I typically use the AICc, it is always important to back up the results of one measurement of fit with the others. Therefore, it is important to check metrics such as ChiSquare, CFI and RMSEA. Typically, we want the lowest ChiSquare value and RMSEA possible and the highest CFI possible. It is unlikely that these metrics won’t align, but if they do not, it could be worthwhile to investigate the models more closely.

Model Comparison
JMP Pro’s SEM platform contains a section for model comparison, which enables us to compare a range of SEM diagrams for the same variables. Comparison is key when using SEM, and all the metrics provided in this section should be used primarily for comparison. This is because there’s no definitive way to say that “this model is the best.” Instead, we use different statistical tests to determine how well the models fit to the actual data. Therefore, we must be careful when using these statistics to validate our model; the statistics could say that the model is a good fit when just looking at one model, but when compared to other models, the initial model might be painfully incorrect. The best way to demonstrate this idea is through an example.
Track and Field Example
To provide an accessible example, I decided to move away from the engineering theme for this series and use a data set on the time to complete running races of different distances. Hopefully, this will also serve as a demonstration of why domain knowledge is so important!

Before I performed this analysis, all the variables were standardized to ensure that the SEM would converge.
In the first model I created, I used two latent variables of “sprinting ability” and “endurance,” with the time taken to complete each race being an indicator of these abilities.


As you can see from the Model Comparison above, JMP Pro has automatically fit an unrestricted and independent model, which my model has been compared to. The AICc weight is 1 for my model, which means that out of the three models, there is a 100% chance that my model is the correct model. So, job done, right? A 100% chance of being correct sounds pretty good, but the key part of that is that it is only correct compared to the other two models.
This is where our domain knowledge is critical. Is it likely that a person’s ability to sprint and their ability to run long distance are independent? Of course not. In fact training for any kind of race is highly likely to improve someone’s fitness levels overall, and so both of our latent variables are likely to be connected in some way. With this in mind, let's create a model that takes this connection into account.
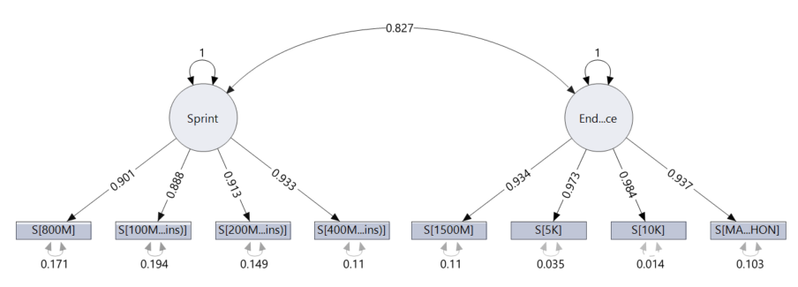

The new model shows that there is a significant correlation between the two latent variables as expected. Now looking at the AICc weight, we can see that out of the four models, our new model is now 100% likely to be the true model. Clearly, this leads us to a few conclusions:
- Firstly, as mentioned before, we cannot just use these statistics to say that our model is correct, only that it is likely correct compared to our other models.
- Secondly, we cannot use just one statistical test to determine how good our model is.
- Finally, just because our metrics tell us that our model is good doesn’t mean that the model is correct; we need domain knowledge to determine whether the model makes practical sense.
For this example, I then altered the model using a few different assumptions to test different models. I have uploaded the example if you want to explore it further, but the final results of the model comparison are reported below. Take care to use the correct columns if using my data set as I had to transform the initial values from seconds to minutes.

I hope this post gave you insight into how we determine how well our models fit our data. I look forward to hearing how you have applied these fit indices to determine the quality of your own models. See you next month!
You can see all posts in my SEM series here.