- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
We often use hypothesis tests for a difference but there are times when we want to test for equivalence. It is not proper to use a result that a difference test was not significant to conclude equivalence. Note that JMP performs some equivalence tests, such as comparing two groups in the Oneway platform.
This script performs a test of equivalent for any parameter that meets the assumptions of a t-test:
- Observations are independent.
- The sampling distribution of the parameter estimates is normal.
Common examples include sample averages and parameter estimates for linear models.
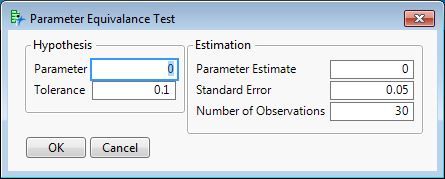
Here is what the initial dialog looks like when you run the script:
The script requires just five inputs:
- The hypothesized parameter value
- The tolerence value - any observed difference from the hypothesized value that is smaller than the tolerance indicates practical equivalence or similarity
- The parameter estimate
- The standard error of the estimate
- The sample size - number of observations used for the estimate
I will illustrate the use of this script with the following example.
- A sample of 100 items with known value (Standard Y) are tested with a new instrument (Test Y).
- The new instrument should provide identical results, so the hypothesized regression slope is 1.
- The practical equivalence is within 5% of the hypothesized value, so the tolerance is 0.05.
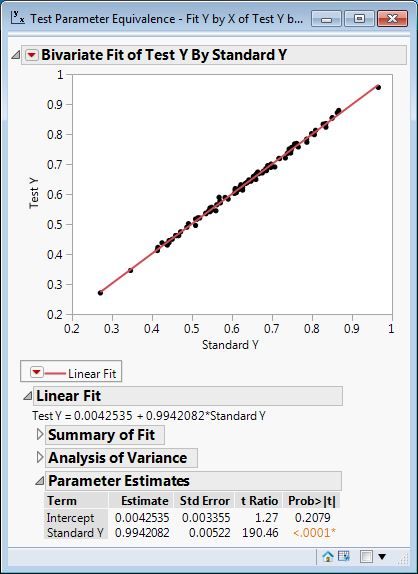
Here is the regression analysis:
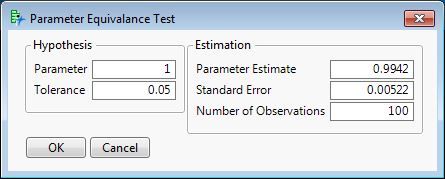
The parameter estimate is 0.9942, the standard error of the estimate is 0.00522, and the number of observations is 100. The values in the dialog are changed to match the situation:
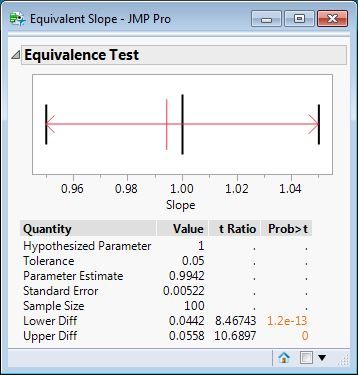
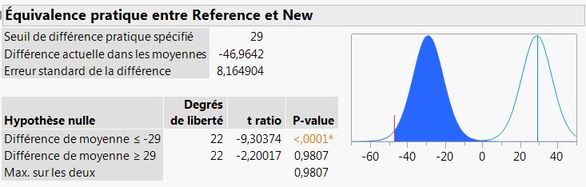
This result appears when I click OK:
The plot shows the hypothesized parameter and the interval of practical equivalence with vertical, black lines. The parameter estiamte is shown with a vertical, red line. The red arrows show the lower and upper differences between the parameter estimate and the lower and upper bounds, respectively. The information below the plot records the values input to the dialog and reports the lower and upper differences, t-ratios, and one-sided p-values. Both tests are signficant at α = 0.05, so we conclude that estimated slope is equivalent to the hypothesized slope.
Is it possible to share the JMP data table used here in this please. It would help me understand and learn this use full test. Thanks.
I attached the example that was used to demonstrate how to use this script as requested.
Hello Mark,
Is there a difference of using the script described above and the Equivalence Test (TOST) under Menu Analysis > Adjust Y by X (refer to screenshot attached)?
Thank you,
Thomas
Both tests are based on two one-sided t-tests. The test in the Oneway platform is to test equivalence of sample means. The script above is to test equivalence of parameter estimates.
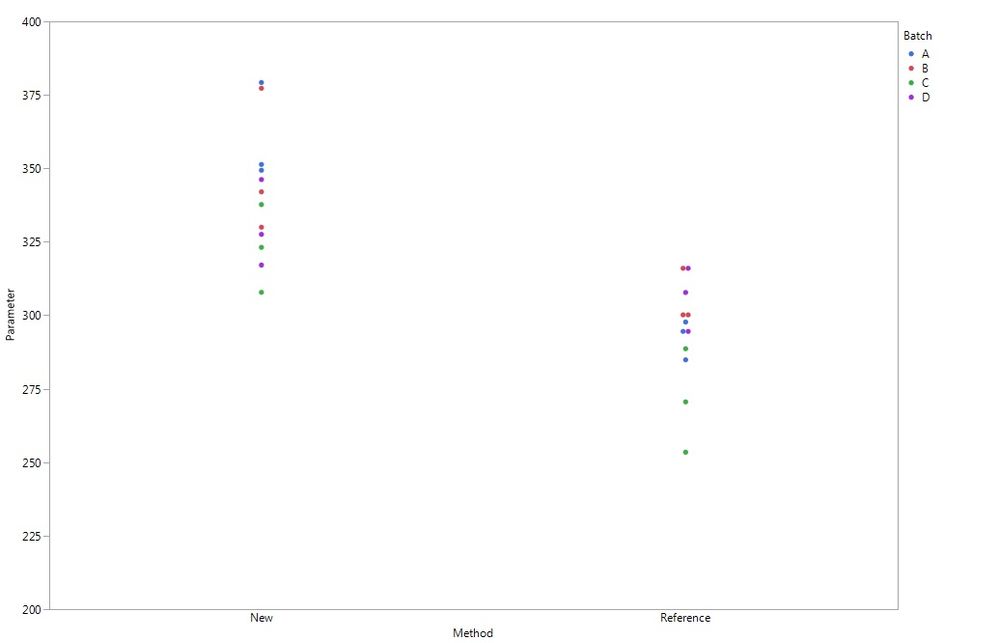
In my case, I want to evaluate the equivalence of two analytical methods over different batches (Refer to graph attached).
I plan to use TOST available in Oneway platform.
But I heard about Bland Altman test in case of my batches would have too different contents. Is this test applicable to compare two analytical methods?
Thomas
The Oneway platform provides the equivalence test. You have two factors, though, method and batch. Is batch your random effect (sample)? If so, then method is the only factor and you are good to go.
JMP provides the Bland-Altman method in the Matched Pairs platform. NOTE: Bland-Altman is a test is for a difference, not for equivalence.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us