In this series of seven blog posts, I have tried to demystify DoE with simple explanations of some of the terms and concepts that can be confusing for people when they are starting out. We have covered a lot. We explained the meaning of confounding, orthogonality and variance inflation. We looked at multiple linear regression, stepwise selection and effect heredity. You have seen full factorials and definitive screening designs (DSDs).
The key takeaways:
- The best way to empirically understand and optimise a process or system is through multivariable models.
- The number of possibilities in multivariable systems is overwhelming.
- DoE ensures you can efficiently collect the data you need.
I hope that you feel motivated to go away and run designed experiments now, if you were not already. Before you do, though, I should add that there is a lot that you might want to learn about that we have not covered here.
What did we miss?
We used an example of an experiment for optimising the LVI set-up in a GC-MS analysis system. We saw why the 26-run DSD was such a useful experiment because of the correlation properties and the model that it enabled us to build. However, we didn’t talk about how this experiment was designed. DSDs are very useful in many situations, but I strongly believe that you should design for the problem that you are trying to solve, rather than engineering your objective to fit with an experimental design. In this blog post, Bradley Jones, co-discoverer of DSDs, talks about situations where DSDs are not appropriate.
With DoE software like JMP, you can use optimal design to create an experiment that is tailor-made to your objective and any special constraints. In our example, we might have been constrained that we could not change liner type between every run because it involves a difficult and lengthy shutdown of the system. In this case, we would need to define this as a hard-to-change factor and create something called a split plot design. Or we could have been constrained that low vent pressure and high injection speed can’t be simultaneously achieved, so we would need to design an experiment that avoids those settings.
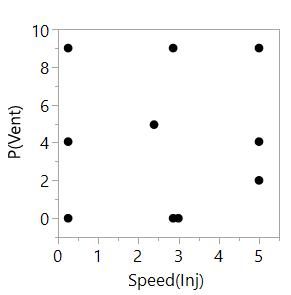 Plot of an optimal design with a constraint on factor combinations.
Plot of an optimal design with a constraint on factor combinations.
The book Optimal Design of Experiments: A Case Study Approach is a great introduction to optimal design once you have mastered the basics of DoE.
We also missed out the important thinking that you need to do before you start designing an experiment. You need to think hard about what the objective of the experiment is, about what factors to include and over what ranges. You also need to be confident in your measurement of the response of the experiment: If you get very different response results from repeat runs at the same settings, then you will not learn much when you start changing the factors according to a designed experiment.
What if I have more than one response?
So far in our example, we have been looking at only one response, PkHt(SUM). Most of the time when you have a process or system that you need to understand, there will be more than one response to think about. With many responses to understand and optimise there is an even stronger need for the efficiency and effectiveness of DoE.
This case is no different. For reliable detection of impurities with our GC-MS system, we need peaks that are both big and symmetrical. So, as well as the PkHt(SUM) response, we also have a measure of the symmetry of the peaks, PkSym, for each run of the experiment.
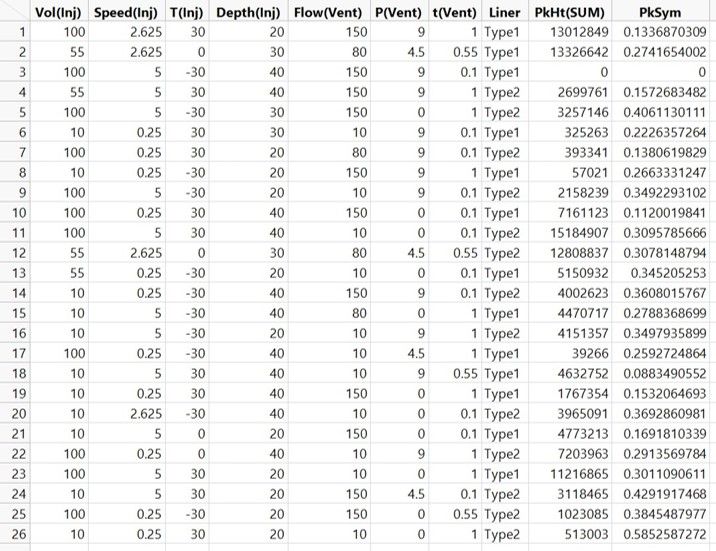 Data table for 26-run experiments with two responses.
Data table for 26-run experiments with two responses.
We want PkSym to be as low as possible and the ideal value is 0, which would mean that the peaks for every analyte are perfectly symmetrical.
Having collected the response data for each run, we can build models and find the best compromise to meet all objectives.
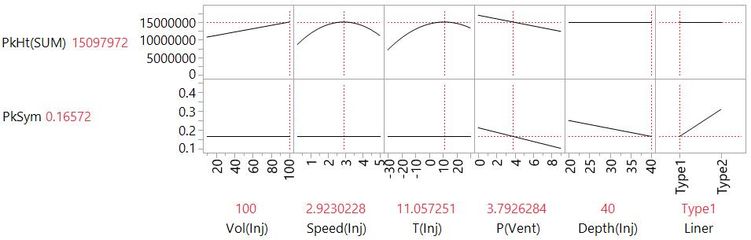 The optimal settings to maximise peak height and quality can be found from modelling the data from the 26-run experiment.
The optimal settings to maximise peak height and quality can be found from modelling the data from the 26-run experiment.
You can see how the DoE advantage is even greater when you have multiple response objectives.
Accelerating innovation
Thanks again for the example here from Jonathan Dunscombe and Camilla Liscio at Anatune. Interestingly, Jonathan was not a believer in DoE before this project:
“I had struggled for quite a while trying to get a working LVI method for this dual solvent system… it was particularly tricky. I wasn’t quite sure what results from DoE I would get, especially as there were many variables and several important factors that needed to be taken into account. What really impressed me was the speed at which the LVI method was optimised and just how reproducible the final method was.”
As Jonathan has seen, with DoE you can accelerate innovation. You can develop the best processes and products in minimum time and with maximum predictability. I hope that this series of blog posts is helpful in spreading this message, so that more people use DoE as their go-to way of learning by experimenting.
Please comment below, particularly if you think there is anything important that I have missed in this series.