Hi all,
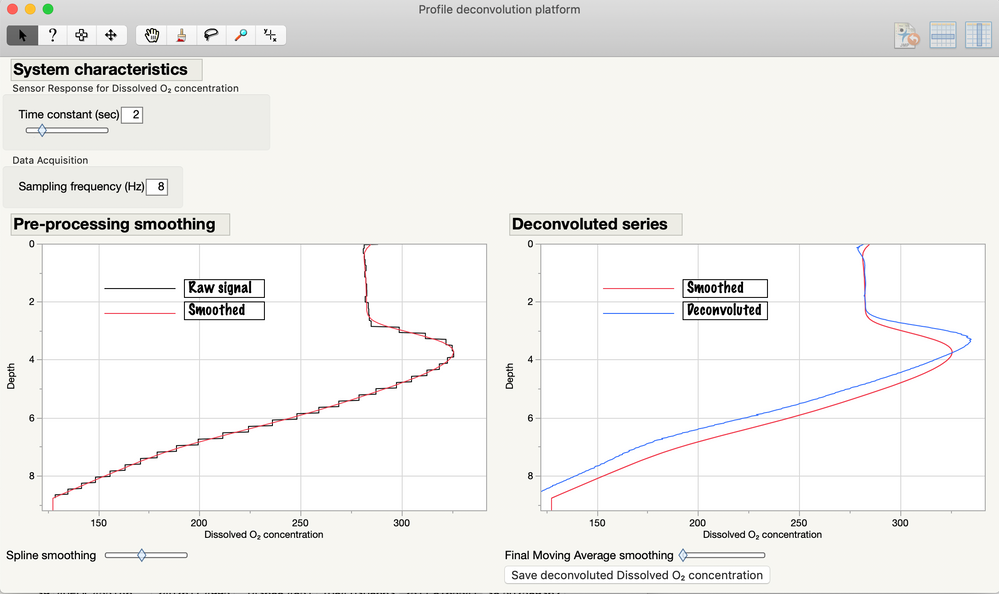
In many fields, it is necessary to take vertical profiles of parameters (e.g. temperature profiles in the ocean or in lakes). This is done by lowering sensors at a given speed and recording the readings at high frequency. However, not all sensors respond very quickly to changes in their environment. While some may be very quick (like temperature, a few milliseconds), others need more time to react and their time response will determine whether a particular profile is accurate or not. In this case, the true vertical profile of a given parameter is convolved with the time response of the sensor. Fortunately, if one knows the time response curve of a sensor, it is possible to get back an estimate of the original signal. This process is called deconvolution. This add-in performs the deconvolution (based on Fourier and inverse Fourier transforms) of profiles where the sensors are known to obey an exponential function response (changes fast at first and slows down asymptotically to the new value). This is the case for most environmental sensors. All one has to do is to select the depth (or time) and sensor variables from a data table and the platform will prompt you to select the sampling frequency (in Hz) of the recorder as well as the time constant of the sensor (in seconds). Two dynamically interelated panels will appear (see screenshot below). On the left panel, the profile of the raw sensor signal will appear as well as a smoothed version of the same signal (in red). This is to smooth out irregularities in the sensor signal that are due to sensor signal resolution (not the time response). You can adjust the degree of smoothness as you feel appropriate. On the right panel, the same smoothed signal will appear together with the deconvoluted signal (in blue). When you are happy with the signals, you can then save the deconvoluted signal. You can also apply a moving average filter on the deconvoluted signal as Fourier deconvolution can sometimes lead to high frequency noise.
Let me know if you would like improvements to it.
Best regards, Yves