- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- what is the meaning of the levels in a 2D contours graph Nonpar Density?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
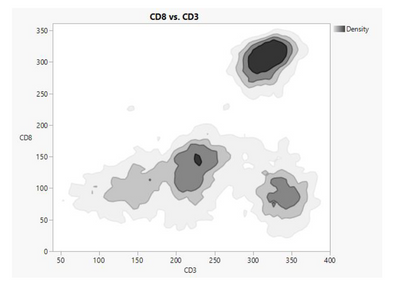
what is the meaning of the levels in a 2D contours graph Nonpar Density?
JMP16 pro.
The default number of levels in a 2D contours graph with Nonpar Density is 4, and one can adjust this number starting from 1.
I can find the meaning of another type of 2D contours graph, which is HDR, which only has two levels, the darkest level is 50% cumulative prob, and the lighter is 99%. But there is no information on the 4 levels in Nonpar Density 2D contours graphs.
What is the meaning of these levels? I guess, are the 4 default levels 25% (darkest), 50%, 75% and 99% (lightest)? What if I change it to 7 levels?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: what is the meaning of the levels in a 2D contours graph Nonpar Density?
"Nonpar Density" stands for "Nonparametric Density Estimate" of a distribution.
Contour plot draws a function f(x,y) in a 3D space on a 2D plane, by connecting dots with the same function values.
Here the nonparametric Density Estimate is a function f(CD3, CD8), which returns a density estimate given a pair of CD3 and CD8 values.
What you guessed for 4 levels is also what I would say as well (except the last 99%, I would rather say it is 100%). Then the first level is corresponding to two circles, and they are corresponding to 25% level, but twenty-five percent of what? So, to be specific, each level of contour line is corresponding to the quantile estimate of the distribution. For example, if you add your data points to the contour (right click mouse in the graph, choose "Add", then "Points"), you should see the two circles should roughly enclose a quarter of your data points. And the last level should enclose all data points. Try number of levels = 1. In general, the levels should be equally spaced. They, otherwise, should be noted to avoid misunderstanding the convention.
In addition, nonparametric density estimate is not unique. It can be changed by changing tuning parameters. In Graph Builder, there is one tuning parameter "smoothness", in Bivariate platform, there are individual tuning parameters for both variables. So I won't read the exact values corresponding to the contour lines literally. Contour lines mainly give me a sense of denseness of data points. And usually I will explore/model the data further.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: what is the meaning of the levels in a 2D contours graph Nonpar Density?
"Nonpar Density" stands for "Nonparametric Density Estimate" of a distribution.
Contour plot draws a function f(x,y) in a 3D space on a 2D plane, by connecting dots with the same function values.
Here the nonparametric Density Estimate is a function f(CD3, CD8), which returns a density estimate given a pair of CD3 and CD8 values.
What you guessed for 4 levels is also what I would say as well (except the last 99%, I would rather say it is 100%). Then the first level is corresponding to two circles, and they are corresponding to 25% level, but twenty-five percent of what? So, to be specific, each level of contour line is corresponding to the quantile estimate of the distribution. For example, if you add your data points to the contour (right click mouse in the graph, choose "Add", then "Points"), you should see the two circles should roughly enclose a quarter of your data points. And the last level should enclose all data points. Try number of levels = 1. In general, the levels should be equally spaced. They, otherwise, should be noted to avoid misunderstanding the convention.
In addition, nonparametric density estimate is not unique. It can be changed by changing tuning parameters. In Graph Builder, there is one tuning parameter "smoothness", in Bivariate platform, there are individual tuning parameters for both variables. So I won't read the exact values corresponding to the contour lines literally. Contour lines mainly give me a sense of denseness of data points. And usually I will explore/model the data further.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: what is the meaning of the levels in a 2D contours graph Nonpar Density?
Thank you. But it can't be 100%, because you can see the nonpara density contours doesn't show the outliers as HDR contours do.
why doesn't the 2D contours graph with Nonpar Density include outliers?
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us