very high r squared interpreting my regression analysis results cubical scheffe polynomial

[#1]

Dear community,

i am using a cubical scheffe polynomial to model my system and i am having difficulties interpreting the analysis for one response. I am posting my analysis results for you to look at. Thanks in advance for your help.

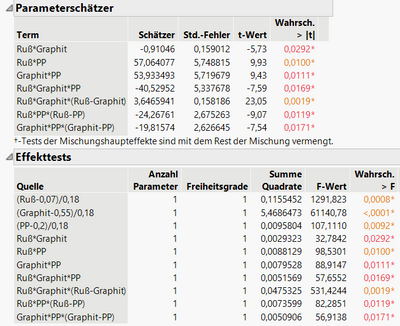
This are estimates for the parametes and the effect tests

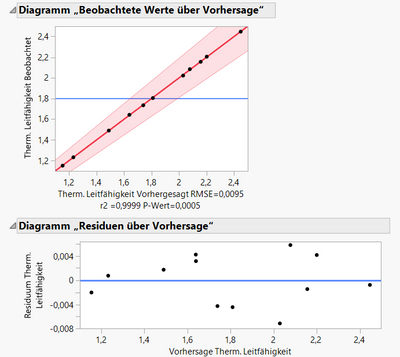
I have a very high r^2 which made me even more suspicious. r^2= 0.999 and of course very small residuals

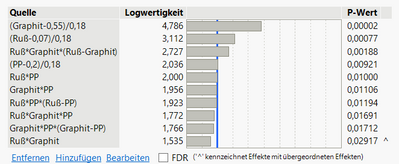
Finally all the terms appear to be significant. Think is why i believe there might be some overfitting at work, but i am not sure. 

[#2 · Accepted solution]

A Scheffe cubic model is used to fit a model to a mixture. In other words, all observations must add up exactly to 1. No rounding errors are allowed. A quick way to check this is to look at the Analysis of Variance table (which is not included here). It should have a message at the bottom stating "Tested against reduced model: Y=mean". If your message says 0 instead of mean, then you are not fitting a mixture model. It is a no-intercept model which would explain some unusual results. That should be fixed before doing anything else.

Once you are sure that you are indeed fitting a mixture model, why are you suspicious of these results? If the results are truly too good to be true, how many degrees of freedom are in your model error? You can see this from the Analysis of Variance table also. A low number of degrees of freedom (which I suspect that you have), could also lead to the model being overfit. You may have close to a saturated model, meaning there are not enough degrees of freedom in the error term to capture the variability of the system. Do you have any replicates in your data? Adding replicates to any set of data will allow you to better estimate the error of the system.

These are just a few ideas. There are lots of other possibilities to explore.

[#3]

Dear Dan,

my system is a mixture but i decided to go with a D-Optimality design. 

I have 11 degrees of freedom. I do not if this is a low number. I will add replicates. Thank you. Should i do that from augment design? 
Do you have any other recommendations for me to explore?

Many thanks for taking the time.

[#4]

From the output I can tell that the analysis is a true Scheffe model, which is good. Although you have 11 degrees of freedom (12 runs), you only have 2 degrees of freedom for error. In other words, your model has 10 terms. There are not many extra runs to estimate the error of the system. However, before adding additional runs (which, using Augment would be a good approach), do you believe the error is really too low? Check your Root Mean Square Error from the Summary of Fit.  That number should be close to the standard deviation of your system when running at steady state. Does it look correct? If it does, then I will ask the question again: why do you think this fit is suspicious? Remember that the tests on the main effects of a Scheffe model are not relevant and should be ignored. You would only look at the tests on the "interactions". Maybe they all really should be significant?

[#5]

Dear Dan, 

thanks again for the taking the time to answer. With the danger of sounding ignorant i will have to ask. How does one check the standard deviation of the system while running at steady state? Is it possible to add replicates manually so (maybe check the corners of the design) so as not to repeat all 12 experiments as they take a long time?

Sincerely

Alex

[#6 · Accepted solution]

I do not know enough about your system to provide an all-encompassing answer. But here are a few possible approaches to determining the standard deviation of the system when running at steady state:

What is the response that you are measuring? Have you evaluated that measurement process? If so, the reproducibility (or possibly repeatability) of the measurement system is a good guide for estimating the standard deviation of the system. This would likely offer the lowest possible standard deviation.

If this is a production process, running the process with absolutely no changes will often yield the standard deviation of the system.

You could make a formulation, divide it into multiple test specimens and measure each one independently to determine the standard deviation of the system. Note that this removes the variability caused by the actual making of the formulation. If that variability might be large, you may want to create several of the same formulation and measure each one. 

One of the key things to consider before running any designed experiment is to perform an evaluation of the measurement system. This would avoid potential problems caused by the measurement system itself. Plus, evaluating that measurement system would provide you with a reasonable idea of the error that you would expect to see from the designed experiment. Thus, it would allow for an appropriate assessment of power for the design given a certain number of runs before you ever perform the experiment. In short, it could help you avoid some of the potential issues/questions about the analysis once the experiment has been conducted.

[#7]

Dear Dan,

thank you very much for your response. The response i am measuring is thermal conductivity and the std. deviation of the process is indeed very low.  But it is not as low as the RMSE of the analysis. This is why i decided to replicate some points (5) so as to try and get a better fit.

Sincerely

Alex