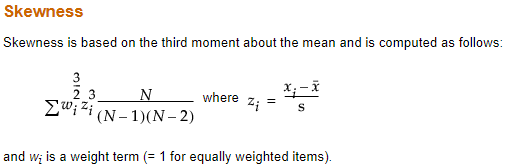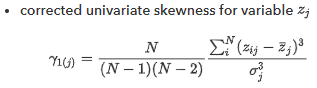- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- t-test
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
t-test
Hello,
Can I get good performance in the t-test for mean comparisons, even if the normality assumption is violated ? (This in the case of comparison of two populations that have similar number of observations for each one (n = 41 and n = 42). I need some references to support this.
Thank you
Adias
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: t-test
The curvature in the normal quantile plot suggests that there is some skew in the population, one of the reasons that the goodness of fit test rejects the normal distribution model. The skew is not that strong, though, so the sample means are approximately normally distributed after all and the t test should be valid.
Here is a reference for estimating the minimum sample size necessary to assure that the sum of the random variables is normally distributed:
Sugden, R. A., et al. (2002) "Cochran's Rule for Simple Random Sampling,
J of the Royal Statistical Society, Series B, Statistical Methodology. 62(4):787-793.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: t-test
If the populations are not normally distributed, the assumption that the sample means may not be violated if the sample size is large enough. The Central Limit Theorem says that the sum of N random variables is normally distributed for large N. The size N depends on the skewness of your population.
In what way and to what extent are the populations not normal?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: t-test
Thank you,
"In what way and to what extent are the populations not normal?"
By plot distribution and Shapiro-Wilk W test (alpha = 0.05). In the figure attached there is an example of the plot and test for one population.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: t-test
The curvature in the normal quantile plot suggests that there is some skew in the population, one of the reasons that the goodness of fit test rejects the normal distribution model. The skew is not that strong, though, so the sample means are approximately normally distributed after all and the t test should be valid.
Here is a reference for estimating the minimum sample size necessary to assure that the sum of the random variables is normally distributed:
Sugden, R. A., et al. (2002) "Cochran's Rule for Simple Random Sampling,
J of the Royal Statistical Society, Series B, Statistical Methodology. 62(4):787-793.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: t-test
Thank you Mr Markbailey for your attention!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: t-test
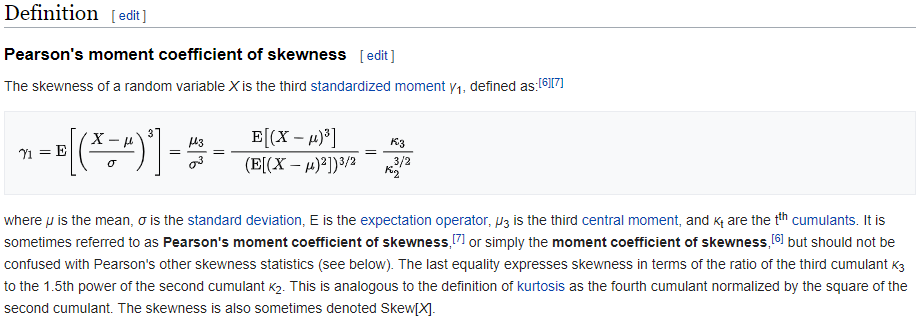
@Mark_Bailey, thanks for providing this interesting reference. Based on your understanding of this article, are G1 and gamma1 one and the same (equal to Fisher's measure of Skewness)? Can you confirm that this is the same statistic that JMP calculates in 'Summary Statistics' (in Analyze>Distribution, for example)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: t-test
I don't know the answer so I looked it up. I am using the definitions that I found in a Wikipedia reference.
JMP Help for Summary Statistics provided by Distribution platform:
SAS/STAT help for PROC CALIS:
Wikipedia source about G1:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: t-test
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: t-test
Without an operational definition of 'good performance' it's impossible to answer your question. If all else fails I suggest any one of the non-parametric tests for testing the hypothesis for two population means. This way you don't have to come up with a definition for 'good performance' and you aren't necessarily tied to any distributional assumptions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: t-test
You could also perform the t test with the Oneway platform (Fit Y by X) and then bootstrap the difference with JMP Pro.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us