- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- rule-extraction algorithms for verify the Artificial Neural Network (ANN)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
rule-extraction algorithms for verify the Artificial Neural Network (ANN)
Hello,
I recently start to use JMP Pro also for the artificial neural network.
I would like to know, how can I verify the neural network architectures with JMP?
E.g., using the mathematical expressions, symbolic logic, fuzzy logic, or decision trees...
I read that this system could resolve the "black box."
Thank you so much,
Angelo
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: rule-extraction algorithms for verify the Artificial Neural Network (ANN)
After you run a model, you can click the red triangle at the top of the outline for that model. You have choices to view the network diagram and you can also show the estimates. The structure of each node depends on your choice of the activation function.
What else do you need?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: rule-extraction algorithms for verify the Artificial Neural Network (ANN)
This quote is from the help portion about the prediction profiler command to output a random table:
So it is a simple way to obtain a uniform random simulation of the predictors and the model prediction of the response. It has the same purpose as the Output Grid Table command.
The Simulator function gives you much more control over the nature of the variation of the predictors and additional random variation of the response. It is primarily for assessing process capability but obviously has other applications.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: rule-extraction algorithms for verify the Artificial Neural Network (ANN)
After you run a model, you can click the red triangle at the top of the outline for that model. You have choices to view the network diagram and you can also show the estimates. The structure of each node depends on your choice of the activation function.
What else do you need?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: rule-extraction algorithms for verify the Artificial Neural Network (ANN)
Thank you so much Markbailey,
Too easy for quickly found ... :)
Satisfied with the JMP software and its support.
Do you know if there are some publication or conference paper that describe the Estimates of ANN in JMP? Because for publicating the data, I have to support my analysis and my publication with the correct reference/s based on JMP.
Regards,
Angelo
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: rule-extraction algorithms for verify the Artificial Neural Network (ANN)
You might search for such references. I don't have any at hand.
Commercial software vendors do not generally publish their numerical methods or code because it is proprietary intellectual property. JMP offers this page as a resource to users to help them establish the quality of JMP.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: rule-extraction algorithms for verify the Artificial Neural Network (ANN)
Hello Mark,
I am pleased to greet you, I am new to JMP, I have some questions:
1. How can you make predictions of future stock prices with JMP neural networks?
Apparently JMP does not have the recurrent neural networks with RNN memory.
2. JMP in the training of the model optimizes the weights of the networks with genetic algorithms or genetic programming?
3. JMP optimizes the number of neurons and the number of hidden layers with genetic algorithms or genetic programming?
I have tried JMP ARIMA to predict future stock price with poor results.
Greetings,
Marco
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: rule-extraction algorithms for verify the Artificial Neural Network (ANN)
This probably should be a new thread as it does not directly relate to the original questions. I'm also not Mark, but I think I can answer your questions.
1. In order to predict a future event, you would need to introduce a time element to your neural network. There are multiple ways to do this. One way is to lag the target variable by one time period. So if your time interval is days, you could use yesterday's inputs to predict today's target. You are correct that JMP does not offer recurrent neural networks.
2. JMP does not use genetic algorithms or genetic programming in the optimization of the weights.
3. No, JMP does not use genetic algorithms or genetic programming in optimizing the number of neurons or number of hidden layers. In fact, JMP does not optimize the number of neurons or the choice of one or two hidden layers. JMP offers an exhaustive search for all of the various settings you wish to attempt. You can then choose the winner.
For these more advanced neural network features, you might want to consider SAS as these techniques are available in SAS as well as Viya.
Finally, please keep in mind that there have been lots of studies of trying to predict stock prices. Studies have shown that short-term stock prices are best modeled as a "random walk" meaning that there is no discernible pattern. In other words, don't blame the modeling technique for not working on a set of data that cannot be modeled well. Good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: rule-extraction algorithms for verify the Artificial Neural Network (ANN)
Hello dan,
I am glad to greet you, JMP seems to me to be an excellent software and every day it surprises me to discover the solution options it offers ..... some questions:
1. The answer of point 1 is interesting (retrace the target variable ... there are several ways to do this), you could detail with examples.
2. I have noticed that the impulse finds the optimal quantity, will there be an option in the neural network platform that optimizes the parameters or hyper-parameters of 1 model? ... that is, learning rate, optimal number of neurons, optimal number layers ... etc
Greetings,
Marco
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: rule-extraction algorithms for verify the Artificial Neural Network (ANN)
The problem with point 1 is that the algorithm for a neural network has no concept of a time axis. That is why a recurrent neural network is often used for time series data since a recurrent neural network does include a sequencing component. Since JMP does not offer that, you will need to create a time or sequence element in the data. I won't be able to give a complete guidance in this forum as this is a large topic. One of the things that you will need to understand is your forecasting horizon. That means, what are the units of time that you will be using, and how far into the future are you trying to predict. My first suggestion was a very simple approach, one day ahead prediction. That approach will not utilize any previous target values, only values of the inputs. But, you could use the previous day's target as an input as well. Then you could try different time lags, depending on how much of the past data you want to use as well as how long your forecasting horizon is. There are likely some other more creative techniques to add a time element to a neural network. Some research will likely turn up some other options for you. Keep in mind that various approaches are needed depending on how often you plan on updating the forecasts, how often you need a forecast, etc.
As for point 2, I don't know what you mean by "impulse finds the optimal quantity". The idea of finding the optimal learning rates, number of hidden layers, number of hidden nodes, etc. is called autotuning. JMP does not offer autotuning. If you look in the JMP community, you should be able to find a JMP script that can assist in autotuning (I seem to remember that somebody did write one). The script truly is a brute force method, meaning that it will try all of the various settings that you specify. Therefore, it can take quite some time. Then based on the results, you choose the best combination.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: rule-extraction algorithms for verify the Artificial Neural Network (ANN)
Hello Dan,
Excellent answer !, some questions:
1. It seems to me that Python has recurrent neural networks, could they be trained in the JMP platform and generate C code?
2. I have a table with 200 columns of stock prices,
How could JMP indicate in 200 new columns with the number 1 the low prices, with the number -1 the highest prices (peaks) and with 0 the rest of the prices?
Greetings,
Marco
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: rule-extraction algorithms for verify the Artificial Neural Network (ANN)
I cannot speak about Python. However, you can run a Python script from within JMP and bring the results back. However, because the prediction formula was created in Python, I do not believe JMP will convert that to C code.JMP can only convert their own native formulas to various formats.
As for the 200 columns of stock prices, the easiest way to do that would be with a script. However, an interaction approach is to do the following:
1) Have your 200 columns to be converted right next to each other.
2) Create 200 new columns by using Cols > New Columns.
3) Select the 200 new columns, which are all empty.
4) Choose Cols > Standardize Attributes.
5) In the standardize Properties section, click on Column Properties > Formula.
6) Check the box for Substitute Column Reference and click Edit Formula.
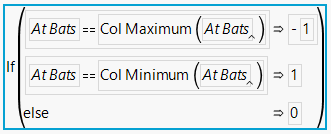
7) Build the formula for the first of your 200 stock price columns. The formula (according to what you specified) would look like this:
8) Click OK to close the formula editor.
9) Click OK again to close the Standardize Columns Attributes dialog.
That formula should be applied to all 200 columns with the appropriate column references applied.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us