- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: "Double weibull"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
"Double weibull"
I have some reliability data regarding a random error, that I can fit to a weibull distribution. But I need to make an reliability analysis of the probability of two of the errors happening consecutively, and as this probability is very small, it it not possible to let the test run until this happens.
So instead, I had the idea to generate some data from the weibull distribution that I have described. I can generate random draws from the weibull distribution, but is there a way to draw from a “double weibull” or in other words a weibull x weibull distribution?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: "Double weibull"
Easy to do. I am assuming that each component or event is independent of each other, and that "failure" is that the time to event is less than a desired time. You can just create two columns in a data table with the Random Weibull() function in the column. Then you can use another column to test to see if both components failed before a given time.
Maybe a simpler way is to just use basic probability calculations. If T1 is the time to failure for component 1, T2 the time to failure for component 2, then the time to failure for both to happen at the same time is Tmax=max(T1, T2). Let F be the cumulative distribution function for T1 or T2 [F(t) = Prob (T1 < t)]. The cumulative distribution function of the maximum of two identically distributed and independent random variables is just Fmax(t) = [F(t)]^2.
To sample from any probability distribution, if you know the cumulative distribution function, you can use this approach.
- generate a random uniform value (uniform random on the interval [0,1]), U
- Find Tmax such that U=Fmax(Tmax) --> this will be your random variable from the "double weibull" distribution
in the cause above, Fmax(t) = [F(t)]^2, so solving for Tmax is just
U=Fmax(Tmax)=[F(Tmax)]^2
sqrt(U) = F(Tmax)
You can use the Weibull Quantile() function in JMP to find Tmax
alpha=1;
beta=1;
// generate random "Double Weibull"
Tmax = Weibull Quantile(Random Uniform(),alpha, beta);You could use that formula in a column in a data table, or make a JMP script to generate the random draws.
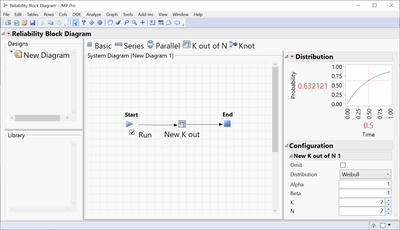
Alternatively, if you have JMP Pro, you can use the Reliability Block Diagram platform to easily see the distribution of failure time for this "K out of N" system.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: "Double weibull"
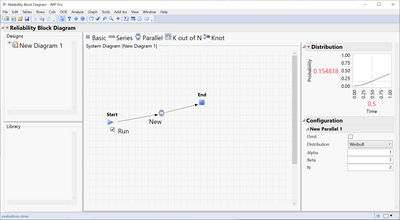
Actually, I think is a parallel system design, not "K out of N"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: "Double weibull"
Thank you for your suggestion, but there are some important prerequisite that are missing. Maybe i should clarify:
I can describe the single error with a weibull distribution, and the probability of an error is very small (one in a million). The system can run if only one error occurs, but I can detect the one error.
But the error I am looking for is when the single error occurs twice consecutively. And as the probability of the single error is so small, I can not run the test until that happens (or simulate two columns of random weibull numbers as it would need a lot more than a million rows) . So i would like to draw a random number from a weibull^2 distrubtion, or somehow simulate this weibull^2 distribution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: "Double weibull"
I don't understand what you mean when you say " I can describe the single error with a weibull distribution". The weibull distribution typically is used for describing the distribution of a "time to an event". So do you mean the error occurs within a given period of time?
Are the errors consecutive, really, in that the 2nd error cannot occur if the first error cannot occur?
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us