- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- proper analyses of count data with factors
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
proper analyses of count data with factors
I have an experiment where fungi were cultured from two different types of plant (A and B). I have identified all the species to species. I want to test to see if there is a statistical difference between the number of times a Fungal species was recovered between the two plant types. I have JMP 17 and thought a generalized linear model would work with plant type and species and their interaction as fixed factors, but I continually am getting error messages. Any ideas? Is there a different way of doing the analyses?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: proper analyses of count data with factors
What are the error messages? How did you design the data collection? Are Plant Type and Species the only two factors? Did you cross them to create the Interaction term in your linear model?
You cannot estimate an interaction term unless Plant Type and Species are independent, like Plant Type = {A, B} and Species = {1, 2, 3}. Can you have the same species in both types of plants?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: proper analyses of count data with factors
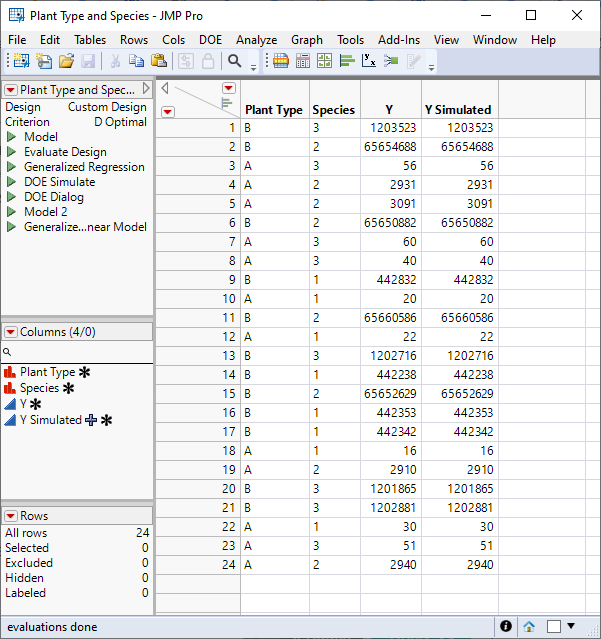
I simulated an experiment with Plant Type and Species as factors. I simulated a response with a Poisson distribution. I attached the data table for you to explore.
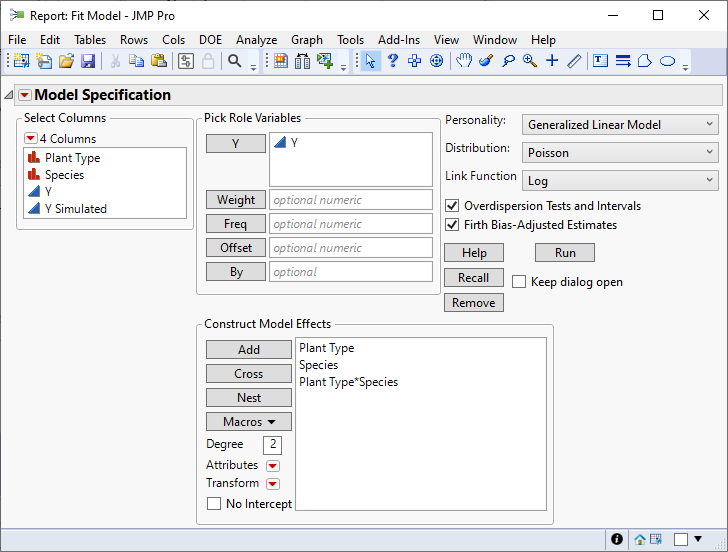
I defined the GLM with an interaction term.
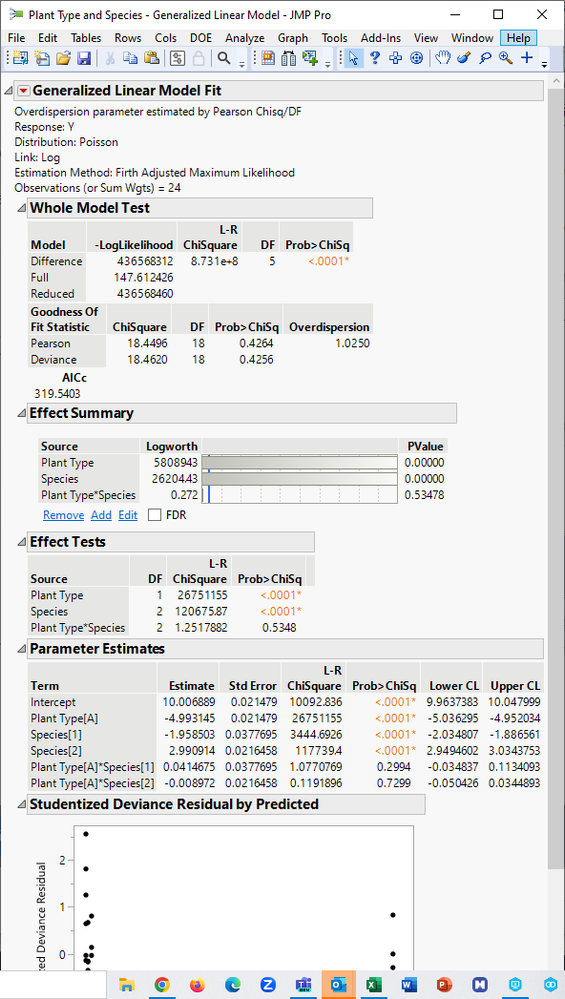
I obtained the default analysis report:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: proper analyses of count data with factors
Thanks and I'll look this over. The plants are two different species in the same field with 25 plants each. We then sampled the foliage and cultured out any fungi present on the leaves. Some fungal species may be present on one species and not another, some on both. The number of times a fungus was isolated (count) is what I am interested in assessing. Basically do we see more or less of species X on plant A, etc.
The fact that I could not control the number of isolates or species recovered per species or per plant means that there are zeros and unbalance to the overall dataset. Perhaps that is causing the error?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: proper analyses of count data with factors
Do you consider the response to be the presence or absence of a fungal species, and you count the number of plants (out of 25) with the fungus?
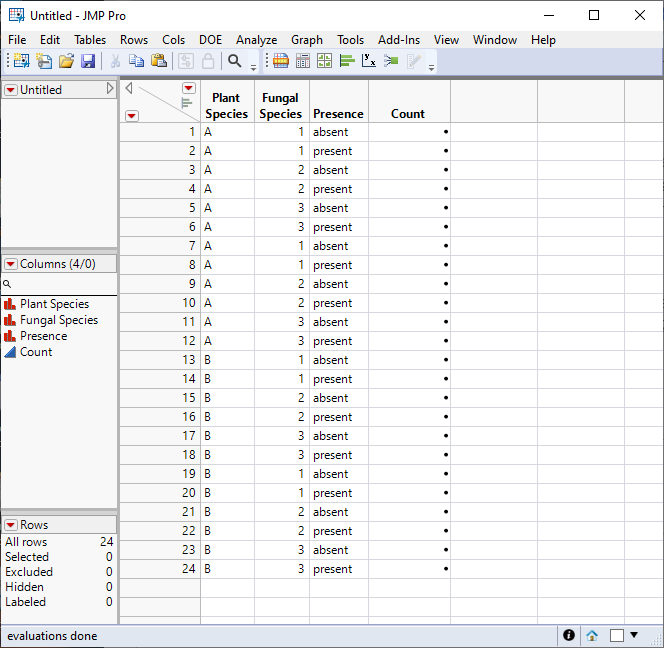
It would be best not to use Poisson distribution in a GLM analysis. Use a Binomial model (absent, present) because you know how many of each. That is, y is the number with fungus and 25-y is the number of without.
Your data table should like like this:
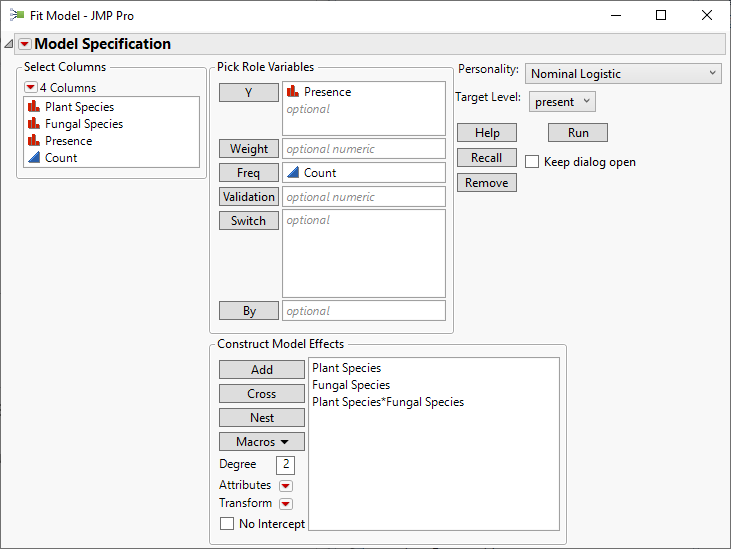
Enter the counts in the last column. I saved a table script to complete the action of selecting Analyze > Fit Model. The launch dialog looks like this:
The data table is attached for you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: proper analyses of count data with factors
Thanks for the idea. I think you are close, but what I have are basically a list of 20 fungal species. Most are isolated from the different plant types at different amounts, so I may have species a 20 in plant a, but 45 in plant b. I want to be able to say with some degree of confidence that a given species is or is not different between the different plants.
I thought a tradtional chi square would work where I have the fungal species analyzed by plant as categorical variables in analyze Y by X but I am not seeing how I can go in and determine the exact species differences. As I interpret it, the chi square being significant would only tell me that across all the species the distribution between plant a and b is different, not which fungal species are different between plant a and b.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: proper analyses of count data with factors
If you have Plant Species and Fungal Species combinations, then a cross-tabulation should work.
Which is it, different or not different? Hypothesis tests work in one direction only: to reject the null hypothesis based on the strength of the evidence (e.g., p-value or confidence interval of a sample statistic). You need to specify your working hypothesis (the alternative) and the null hypothesis (not yours).
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us