- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: paired t-test with censored data
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
paired t-test with censored data
Hello, I have microbial count data (log 10) that is censored. The desire is to compare a Test period to a Baseline, and determine if there's a statistically significant reduction in microbial counts. From what I can see, only Gen Reg can do censored data and use a Blocking factor. The blocking factor is the only way I can think of to link the paired Test and Baseline results. But I seem to not have enough degrees of freedom to perform the test? And the blocks don't make sense to me, the way JMP interpreted them? Any suggestions?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: paired t-test with censored data
Let's start with your data. It has problems.
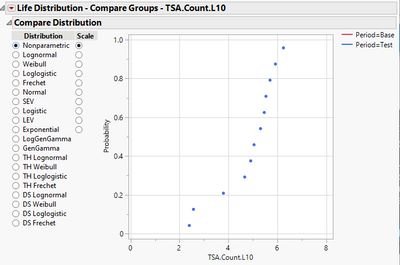
According your statement of the desire, I did a comparison of the nonparametric distribution estimates of the two periods.
And this is the result:
Do you see the problem? Base period does not have a nonparametric estimate.
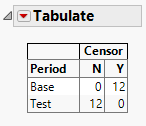
This tabulate your data by Period vs Censor. And seems all your Base period observations are censored. Test period observations are not.
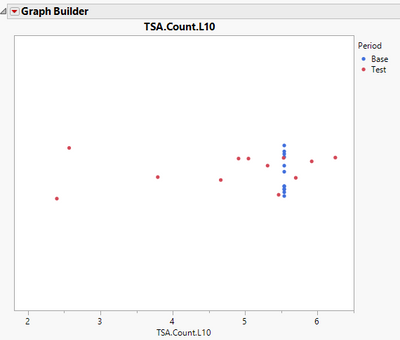
This is a dot plot of your data, colored by Period. All Base observations have the same value.
Assume the data don't have above issues. Now is the question, If you want to compare the two periods, why do you add Block? Is it an explanatory variable that can describe the differences between the two periods? The decision to put it into the model should not depend on whether a statistic can be produced. So I suggest just removing Block from your model, and see whether the results make sense to you, assuming the data is good.
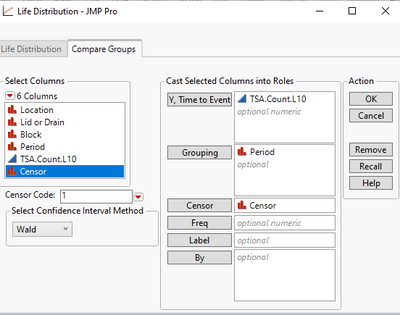
Besides GenReg, two other platforms may help you study data with censored observations with a grouping variables: Life Distribution with grouping (first screenshot above), and Fit Life by X. The two might be more appropriate, if all you need is to compare groups of observations.
But in the end, your data have serious problems. Please don't bulldozer the data by running software and be happy with the result. Could be dangerous.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: paired t-test with censored data
Thanks for correcting the data. I think I understand the problem better.
First, let me answer the last question. If you supply a Censor column, the software assume that it indicates right censoring using the Censor Code of your choice in the launch dialog. That is the convention followed by all JMP platforms that involves censoring. If you want express different type of censoring, e.g. Left Censoring, you have to follow a convention to create data differently. This talk might be the most helpful: Introduction to the Analysis of Censored Data .
I cannot find that GenReg supports paired-test in the documentation. I will appreciate it, if you can point to the location. On the other hand, I will to use other tools to address this problem.
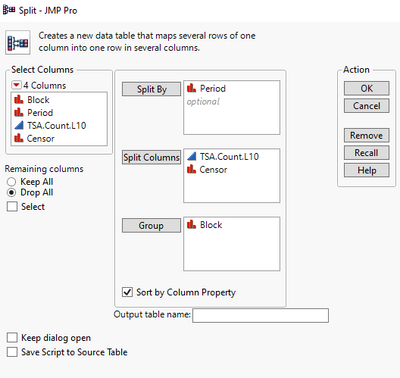
First I split the data to form a new one:
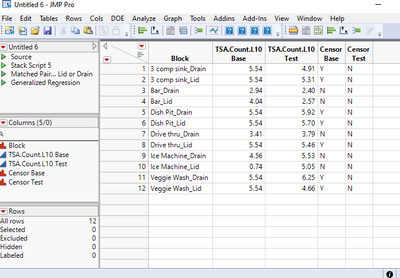
And here is the result:
If one would have done a paired t-test, if no data are censored, one would first calculate the pairwise differences of individual rows. Then the question becomes whether the differences are no different from zero. But we have censored data. I am assuming the right censoring on-wards. Otherwise, change the calculation accordingly.
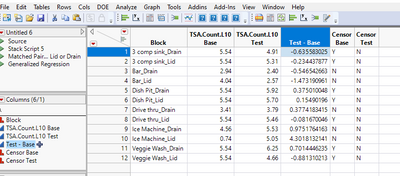
First, I am going to create a column as Test - Base, as one would do for paired t-test.
Now look at the values, i.e. differences, and think what they mean. Look at the first row: 4.91 - 5.54 = -0.635583025471626. Here 5.54 is censored, which means the actual value is greater than 5.54. So the actual difference will be less than -0.635583025471626. Therefore, this makes -0.635583025471626 a Left Censored observation.
And the same logic applies to all rows where Base observations are censored. If Base observations are not censored, the differences are exact values.
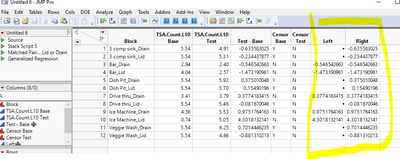
Now create two new columns, as what was said here: Introduction to the Analysis of Censored Data .
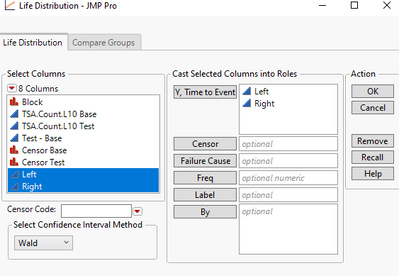
For individual rows, if Left is Missing, Right is not, that is a Left censored observation. If both Left and Right are not missing, and they equal, that is an exact observation. Use the Life Distribution as follows:
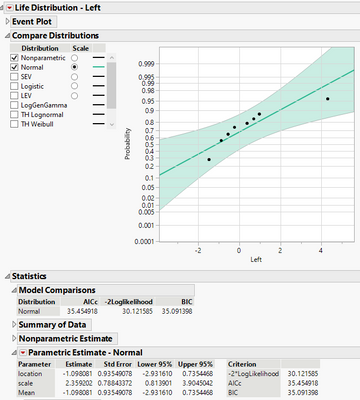
Then fit a distribution, and Normal looks good to me.
Now the question becomes whether the location parameter estimate is significant different from zero. If the answer is yes, then the two groups are significantly different. No, otherwise. In this example, assuming I guessed corrected that the censoring in the data means right censoring, then two groups look no significant different. If I guessed incorrectly, the censoring type of the differences would had been right censoring. Then change the steps accordingly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: paired t-test with censored data
Let's start with your data. It has problems.
According your statement of the desire, I did a comparison of the nonparametric distribution estimates of the two periods.
And this is the result:
Do you see the problem? Base period does not have a nonparametric estimate.
This tabulate your data by Period vs Censor. And seems all your Base period observations are censored. Test period observations are not.
This is a dot plot of your data, colored by Period. All Base observations have the same value.
Assume the data don't have above issues. Now is the question, If you want to compare the two periods, why do you add Block? Is it an explanatory variable that can describe the differences between the two periods? The decision to put it into the model should not depend on whether a statistic can be produced. So I suggest just removing Block from your model, and see whether the results make sense to you, assuming the data is good.
Besides GenReg, two other platforms may help you study data with censored observations with a grouping variables: Life Distribution with grouping (first screenshot above), and Fit Life by X. The two might be more appropriate, if all you need is to compare groups of observations.
But in the end, your data have serious problems. Please don't bulldozer the data by running software and be happy with the result. Could be dangerous.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: paired t-test with censored data
as Peng, thank you - my logic is faulty for labeleing observations as "Y" or "N" in the Censored column. "Y" should occur where the Period = Base and the TSA.Count.L10 = 5.54. The formula I used is below. But now I realzie it's not working, so I just coded the censored data by hand. also, when I stacked the data, I somehow made all of the Base values = 5.54, which is not correct. I probably did that when I was tryin to write the Censor formula.
The reason for the block factor is that this is really a paired t-test. The comparison is TSA.Count.L10 for the Base vs. Test Period, within each piece of equipment, e.g within the Ice Machine + Lid. I would use the Paired T-test platform directly, but it doesn't account for censored data. Gen Reg does. The blocks then designate the paired comparisons, at least that was my hope.
Question: the data is right-censored -- how does the Gen Reg platform know which side the censoring is on?
If( :Period == "Base" & (:TSA.Count.L10 == 5.54),
"Y",
"N"
)- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: paired t-test with censored data
Thanks for correcting the data. I think I understand the problem better.
First, let me answer the last question. If you supply a Censor column, the software assume that it indicates right censoring using the Censor Code of your choice in the launch dialog. That is the convention followed by all JMP platforms that involves censoring. If you want express different type of censoring, e.g. Left Censoring, you have to follow a convention to create data differently. This talk might be the most helpful: Introduction to the Analysis of Censored Data .
I cannot find that GenReg supports paired-test in the documentation. I will appreciate it, if you can point to the location. On the other hand, I will to use other tools to address this problem.
First I split the data to form a new one:
And here is the result:
If one would have done a paired t-test, if no data are censored, one would first calculate the pairwise differences of individual rows. Then the question becomes whether the differences are no different from zero. But we have censored data. I am assuming the right censoring on-wards. Otherwise, change the calculation accordingly.
First, I am going to create a column as Test - Base, as one would do for paired t-test.
Now look at the values, i.e. differences, and think what they mean. Look at the first row: 4.91 - 5.54 = -0.635583025471626. Here 5.54 is censored, which means the actual value is greater than 5.54. So the actual difference will be less than -0.635583025471626. Therefore, this makes -0.635583025471626 a Left Censored observation.
And the same logic applies to all rows where Base observations are censored. If Base observations are not censored, the differences are exact values.
Now create two new columns, as what was said here: Introduction to the Analysis of Censored Data .
For individual rows, if Left is Missing, Right is not, that is a Left censored observation. If both Left and Right are not missing, and they equal, that is an exact observation. Use the Life Distribution as follows:
Then fit a distribution, and Normal looks good to me.
Now the question becomes whether the location parameter estimate is significant different from zero. If the answer is yes, then the two groups are significantly different. No, otherwise. In this example, assuming I guessed corrected that the censoring in the data means right censoring, then two groups look no significant different. If I guessed incorrectly, the censoring type of the differences would had been right censoring. Then change the steps accordingly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: paired t-test with censored data
Thank you Peng, I understand your solution and that is exactly what I was looking for. Also, my earlier wording was a bit vague: I was trying to say that Gen Reg works with censored data, but not with paired data. regards, Paul
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us