paired t-test with a covariate

[#1]

My dataset consists of #of fish caught in three different types of wetland vegetation. This data was collected at 16 different sites. I have done the Wilcoxon signed Rank test in the matched pairs analysis to see if there are signifcant differences in the number of fish caught in the different vegetation types. I am also interested in using water depth as a covariate. Is that possible while within the matched pairs analysis?

[#2]

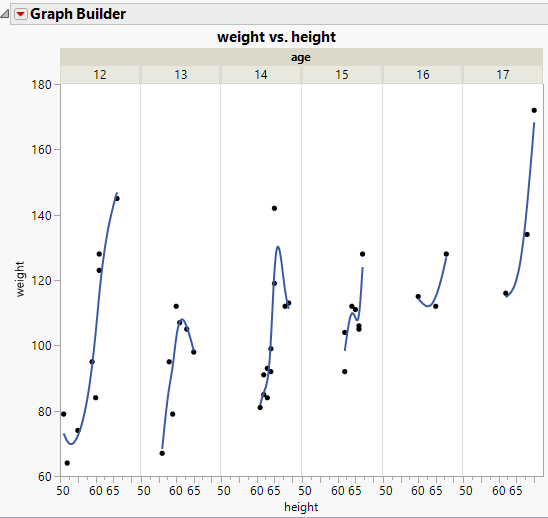
First of all, do you have an indication that the depth of water might influence the response? For example, if you plot the difference versus depth and overlaid by type of vegetation in Graph Builder, do you see an effect like below with another data set?

Or, for example, in your matched pairs analysis, do you see the differences in a horizontal pattern or do you see a pattern such as this:

A horizontal pattern would not suggest another influence but a slanted pattern like that one shown above would.

Unfortunately, Matched Pairs does not provide a way to include a covariate in the analysis. You could fit a model with the covariate, compute the residuals, and then use them as the response in your matched pairs analysis as before. This way allows you to obtain the non-parametric test.

Unfortunately, Fit Least Squares does not provide the non-parametric tests. It assumes a normal distribution of the errors. It does allow you to simultaneously model the effects of vegetation type and water depth, though. You can examine the residuals to determine if the errors seem to seriously violate the regression assumptions. If they don't, then you can use the parametric tests instead. If they do, then you could first transform the response to see if that change helps. The Box-Cox Transformation facility can help determine a good transform.

Since your response is a count of the fish, you might consider using a Poisson log-linear regression analysis instead. Change the personality in Fit Model dialog to Generalized Linear Models, select Poisson for the distribution and accept the default log (canonical) link function.

Note that if you decide to use something other than Matched Pairs, you will have to compute the difference between the paired observations as the response for the other types of analysis.

Let us know if this reply helped at all and if you need further help once you decide on a direction.

[#3]

Thanks Mark for the timely and thorough response. Yes, I did find that there was a significant relationship between water depth and a number of the biological metrics that were calculated from the fish data so I wanted to make sure that the when I am doing the matched pairs and there is a difference between the different veg types that it is not due to the fact that the different veg stands are often naturally found at different depths. Are there different fish in the veg types because they prefer that veg as habitat, or because they prefer that depth? I might also do some ANCOVAs to look at that, but it wouldn't be looking at matched pairs unfortunatley. 

I will give your suggestions a try :)

[#4 · Accepted solution]

What is the nature of the 'pairs' or pairing? How are two observations paired for comparison?

As I said, you could compute a difference column and then use the difference as the response. This approach is effectively a 'matched pair' or 'paired' comparison/test/model.