nonlinear vs fit curve giving different results?

[#1]

Hello - I believe that, if I go through either the "nonlinear" or the "fit curve" options, I should end up with the same result (JMP 15.0). I'm trying to use the built in 4 parameter logistic model from the model library, and fitting a number of different variables by strain (where "strain" is a number of different genetic backgrounds).

For some of the strains, the 'fit curve' and the 'nonlinear' approaches give, as I would expect, identical results - BUT for some of the strains, the 'nonlinear' approach does not fit the data correctly. Even though I make sure that the initial starting parameters are very close to a best fit (by eye), for the strains where it doesn't work, it either won't fit at all, or converges on an answer far away from where it should be. It gives an error message saying: "Warning: xx missing models", but there are definitely no missing data. Does anyone have a fix for this please (ideally without having to use scripting), or can tell me where I am going wrong?

many thanks!

[#2]

Why would you use the Nonlinear platform if the Fit Curve platform fits the desired model?

Fit Curve includes heuristics about each of the models that it supports. It is easier to use and more powerful for a set of models but otherwise inflexible. The Nonlinear platform is more powerful and flexible but does not have any heuristics, so it is up to you to handle all of the details. That is the reason that Fit Curve was created. It eases the burden on you.

Nonlinear regression is a numerical optimization or search technique. It is not a closed form computation like linear regression. You should not expect the results to exactly agree unless every detail at the start is identical and the same algorithm and its implementation are used.

[#3]

thanks for responses!

"Why would you use the Nonlinear platform if the Fit Curve platform fits the desired model?"

Because the nonlinear platform is quicker to use when I have several variables to fit and each variable is fitted by several groups. The nonlinear platform also allows me to calculate confidence intervals for the model parameters, which the fit curve doesn't - this last is really useful as I am using the CIs as part of the visualisation of the output.

"You should not expect the results to exactly agree unless every detail at the start is identical and the same algorithm and its implementation are used."

OK, fine. BUT the results do agree, exactly, between the two platforms, EXCEPT (I've now found, on closer inspection), for just one of the groups, where the nonlinear platform fails to fit it correctly, across all of the variables. I can't see why this is - I will try creating a new jmp file with just that group in it, to see if I could manage to fit it that way, but I would like to understand, if possible, just why that group is misbehaving. (It's not an outlier in terms of the data, so it's not that I am just further away from finding a minimum compared to the other groups.)

thanks again

[#4]

Hi @Jake_b ,

  I won't comment here on which platform is best to use or not, @Byron_JMP and @Mark_Bailey are experts in JMP, so I'd follow what they are talking about. I wouldn't be too surprised if each platform had a slightly different algorithm behind when it comes to fitting models, and hence I wouldn't be too stuck on whether or not they match up. For example, in theory you should be able to get a the same answer in both the boosted tree and bootstrap forest platforms if you set all the parameters appropriately. However, the underlying algorithms are different, so the actual prediction formulas will be a little different.

  Out of curiosity, do you actually have a theoretical model/formula that you can use in the Nonlinear Platform, or are you using something else for the X, Predictor Formula?

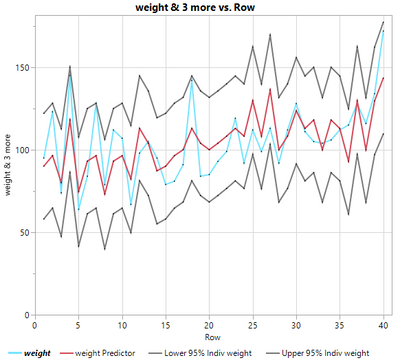
  That being said, you should still be able to get the prediction CIs from the Fit Curve platform, albeit with some extra steps. For example, if you take the Big Class.jmp file and fit :weight by :height in the Fit Curve platform, you can save the prediction formula to the data table. Then, if you do a Fit Y by X (Y= actual, and X=predicted), you can use the drop-down hot button next to "Linear Fit" and save the "Indiv Confidence Limit Formula", which saves the +/-95% confidence interval of the fit. You can the go Graph>Legacy>Overlay Plot, then select the actual, predicted and +/-95% CIs, and you can get a figure like the one below. By the way, I fit the :weight & :height with a logistic 4P model from the Fit Curve platform.

  So, if it makes more sense to use the Fit Curve platform, this is at least a way to go about it so you can visualize the results.

  Just something to think about at least.

DS

[#5]

Thanks for the response -

Firstly, i did have another look at Fit Curve, following the advice above. I see on looking more closely that it DOES give CIs, and, by using the categorical variable to define “group”, rather than “by” (as I was doing before), it’s even easier and quicker to use. So, I have switched to using the fit curve platform - I only had to resort to the nonlinear platform for one data subset (where I had to adjust the convergence criteria to get a reasonable fit).

So, yes, I’m genuinely grateful for the helpful and almost immediate responses about the fitting options; however, just to point out that I wasn’t being completely unreasonable in the first place, no one addressed my original problem: that one of the data groups was not behaving properly with the nonlinear platform. It’s no longer a problem, but I do think that it was a minor bug - I shouldn’t have been able to get different outcomes by resaving the same data under a different file name. Never mind- I have two ways around it now.

[#6]

Based on your description, as much as I can understand of what you've done it does sound like there might be an issue here. Is it possible to share a data table that demonstrates the difference you're seeing between the platforms, and between saving the group to its own data table?

If not here, can you share something with Tech Support (support@jmp.com) so we can investigate more fully?

[#7]

PS forgot to answer your direct question sorry! I’m trying to model bacterial consumption of metabolites. They are not quite simple symmetrical sigmoids - but close enough that the fit is useful, and I think that introducing more parameters would ultimately not be helpful.

[#8]

The two different platforms almost have different functions. Fit curve is super handy when I want to fit typical models quickly, and Nonlinear is more useful when I have a custom function, like something I find in a research paper that isn't main-stream and I want to solve for a set of parameters. 

The iterative numerical optimization used to solve for the parameters in either platform is pretty different that solving a least squares regression. A lot of other software use a pile of hidden assumptions rather than giving you all the levers and button like the nonlinear platform.

[#9]

My results for Fit Curve vs Nonlinear for an exponential 3P function give same parameter estimates to the number of digits shown,  but different confidence limits. When using Custom Inverse Prediction, same happens: same predicted X and Std Error to number of digits shown (6 significant digits) but different upper and lower limits that disagree in the 3rd significant digit. To document these differences, how can I find out the algorithms used for the conf limits in Fit Curve vs Nonlinear?

[#10]

See this page for information about the CI provided by Nonlinear.

The statistical details for Fit Curve do not present any information about the CI. I suspect that they are simply Wald intervals because the Chi square value is provided with the estimates. The Wald interval estimate (Fit Curve) usually does not provide the desired coverage as well as the likelihood-ratio estimate (Nonlinear).