- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: looking for a platform to handle harmonic oscillation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
looking for a platform to handle harmonic oscillation
Specifically looking for a curve fitting platform for underdamped oscillation
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: looking for a platform to handle harmonic oscillation
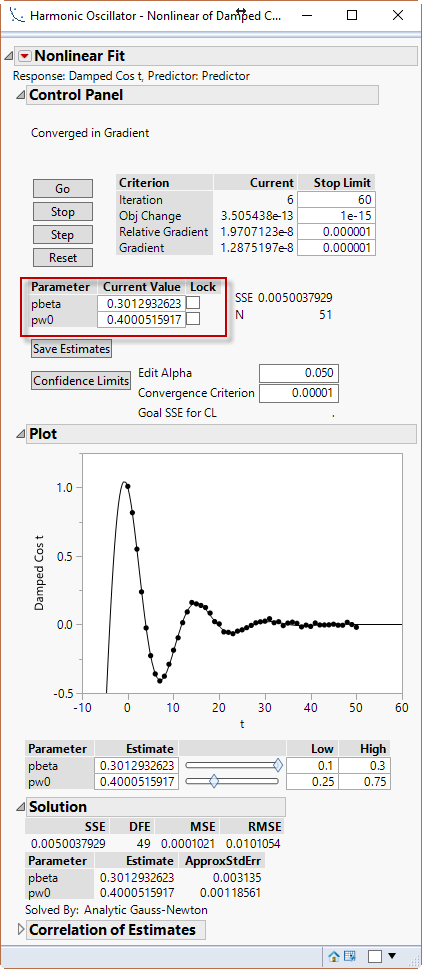
Are you trying to just plot an underdamped oscillator? Or are you trying to fit beta and w0? The below script will actually fit.
Names Default to here(1);
dt = New Table("Harmonic Oscillator",
New Table Variable("beta", .3),
New Table Variable("w0", .4),
New Column("t", set values(0::50)),
New Column("Cos t", formula(Cos(t))),
New Column("Damped Cos t", Formula(
exp(-:beta*:w0*:t)*cos(:w0*t) + random normal(0, .01) //just adding noise
)),
New Column("Predictor",
Formula(
Parameter({pbeta = .2, pw0 = .5},
exp(-pbeta*pw0*:t)*cos(pw0*t)
)
)
)
);
dt << Nonlinear( Y( :Damped Cos t ), X( :Predictor ), Newton );
To give you this. notice how my actual beta/w0 was .3/.4 but I started my predictor with .2/.5
Is this sort of what your'e looking for?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: looking for a platform to handle harmonic oscillation
In JMP 13, have you looked at
Anaylze==>Specialized Modeling==>Fit Curve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: looking for a platform to handle harmonic oscillation
Hacking through that now - thanks. My data should create a an exponentially decaying sinusoid. Trying to figure out how to make JMP do it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: looking for a platform to handle harmonic oscillation
You can give custom equations and parameters in the nonlinear platform. Also Under specialized models.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: looking for a platform to handle harmonic oscillation
Thanks y'all. I appreciate the suggetions. I was able to answer my client's question by fitting an exponential decay curve through my data rather than generate the oscillating underdamped plot. I would like to figure that part out though. I need to find some examples to learn from. Thanks again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: looking for a platform to handle harmonic oscillation
Are you trying to just plot an underdamped oscillator? Or are you trying to fit beta and w0? The below script will actually fit.
Names Default to here(1);
dt = New Table("Harmonic Oscillator",
New Table Variable("beta", .3),
New Table Variable("w0", .4),
New Column("t", set values(0::50)),
New Column("Cos t", formula(Cos(t))),
New Column("Damped Cos t", Formula(
exp(-:beta*:w0*:t)*cos(:w0*t) + random normal(0, .01) //just adding noise
)),
New Column("Predictor",
Formula(
Parameter({pbeta = .2, pw0 = .5},
exp(-pbeta*pw0*:t)*cos(pw0*t)
)
)
)
);
dt << Nonlinear( Y( :Damped Cos t ), X( :Predictor ), Newton );
To give you this. notice how my actual beta/w0 was .3/.4 but I started my predictor with .2/.5
Is this sort of what your'e looking for?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: looking for a platform to handle harmonic oscillation
Exactly!!! You hit a grand slam! Many thanks!!
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us