- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- k-factors for tolerance intervals
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
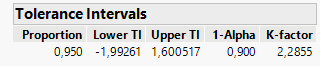
k-factors for tolerance intervals
Hi all,
the k-factor JMP uses for the upper/lower tolerance intervals are different from the ones we use in our company. Does anyone know where the k-factors of JMP are taken from? And can I get the whole k-factor tables?
I am supposed to change the tables which our company uses to the JMP tables.
Thanks
Katharina
- Tags:
- windows
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: k-factors for tolerance intervals
The formulas are described here https://www.jmp.com/support/help/en/16.2/index.shtml#page/jmp/tolerance-intervals-2.shtml#ww1685553
These come from
Meeker, W. Q., Hahn, G. J., and Escobar, L. A. (2017). Statistical Intervals: A Guide for Practitioners and Researchers. 2nd ed. New York: John Wiley & Sons.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: k-factors for tolerance intervals
removed
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: k-factors for control limits
Sorry, I wasn't talking about control charts at all. Translation mistake from my side. I need information about tolerance intervals. I have updated the original post.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: k-factors for control limits
Hello: For a one-sided tolerance interval, no approximation for K is necessary; it is based on the non-central t distribution (and well documented); for the one-sided, if yours don't match JMP's, then yours should be revisited. That said, there are approximations for K that do not make use of the non-central t distribution for users of software that do not have non-central t capability...like Excel for example. For two-sided tolerance intervals, however, there are many approximations (as there is no exact closed form expression). JMP, however, looks to solve for K directly (rather than using some approximation). See the following link. So, if yours is some closed form expression (i.e., some mathematical/statistical formula) it is an approximation and will be different...hopefully still fit for purpose though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: k-factors for control limits
Also, there is some good discussion here (https://www.itl.nist.gov/div898/handbook/prc/section2/prc263.htm) to expand on my post above.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: k-factors for tolerance intervals
To clarify further...if you are tasked with "...change the tables which our company uses to the JMP tables", that will not be possible via some mathematical formula. And if you google something like " tables of tolerance factors for normal population", you will get all kinds of tables that are limited to certain values of confidence, coverage, and sample size. And, many, if not most, of those will be based on some approximation rather than how JMP does it. That said, for "large" samples the difference between methods of calculating K should be negligible from a practical point of view. So, may I suggest a "fit for purpose" solution (see some of my other links) rather than trying to match JMP...which won't happen without some very sophisticated mathematical hoops to jump through (no pun intended).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: k-factors for tolerance intervals
To extend this further still, the link below is what I found via a google search. I'm not in position to vouch for the method therein, but I post it here so you can see what you are up against...or perhaps see a path forward to your ultimate goal.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: k-factors for tolerance intervals
The formulas are described here https://www.jmp.com/support/help/en/16.2/index.shtml#page/jmp/tolerance-intervals-2.shtml#ww1685553
These come from
Meeker, W. Q., Hahn, G. J., and Escobar, L. A. (2017). Statistical Intervals: A Guide for Practitioners and Researchers. 2nd ed. New York: John Wiley & Sons.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: k-factors for tolerance intervals
Hi Sam: In the link you provide, for the two-sided case it says the following (see below). It implies JMP solves the 2nd equation for K, rather than use a formula (an approximation). Can you clarify? Thanks much.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: k-factors for tolerance intervals
I have the statistics book now. It contains tables that have the same factors than JMP uses (I compared random samples).
I can use this to argue that we use JMP, even if we use a combination of input data (like number of observations) that is not in the tables.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us