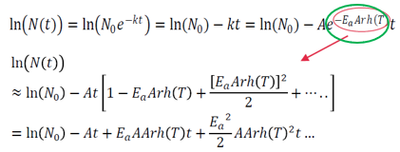- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: estimates in multipule regression
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
estimates in multipule regression
Hello,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: estimates in multipule regression
@MRB3855, I am amazed at this coincidence. Very basic question for you, very difficult for me: If I add the terms you suggest, I will have an approximation of the Arrhenius equation? Also, what other information in this presentation is too incomplete to allow direct use by a novice model fitter?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: estimates in multipule regression
Hi @Ressel : To follow up, here is my take (in no particular order):
1. Keep in mind that the Arrhenius equation (page 12) shows the relationship between the slope and the temperature. So, k is the slope at a given temperature. As you can see on page 7, the slope (k) gets steeper with increasing temperature.
2. Generally speaking (and speaking as a statistician), it's rare that you would not include the lower order terms when there are interactions which include those terms. However, this is one of those rare cases where you would not include those terms. That is because they are using a Taylor series (actually a Maclaurin series, which is a special case of a Taylor series) approximation for k; they did not have to do this; in principle, they could have used the first equation below (from page 16) directly. But that is a nonlinear model and would be more cumbersome. The red circle below really should encompass the entire exponential portion of expression for k (as shown by my green circle). The term in brackets is then the Taylor series approximation for k/A (it actually goes on infinitely, but the idea is that the first few terms will get you close enough). Using this approximation they can use the all the benefits of a linear model. If you look carefully at the first equation below, it is just the equation of a straight line, with the slope, k, replaced by the Arrhenius equation.
3. On page 17 they recommend centering Arh(T); this is a good idea for interpretation of the coefficient A; i.e., create a variable, Arh(T) - Arh(T0), to use in your model (rather than Arh(T) directly).
4. There is more to talk through perhaps, but I'll leave it here for now. The link below may be of some help (in particular, see the last example in the Example section).
https://en.wikipedia.org/wiki/Taylor_series
.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: estimates in multipule regression
Thanks Julian for the immensely detailed and helpful answer. I consider the problem solved now.
Also thanks mpb for the helpful tip
- « Previous
-
- 1
- 2
- Next »
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us