- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: estimates in multipule regression
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
estimates in multipule regression
Hello,
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: estimates in multipule regression
Try this:
When filling in the Fit Model dialog, in the upper left corner of the dialog window there is a red triangle right next to the words "Model Specification". Click on that red triangle to bring up a context menu which includes as its first entry "Center Polynomials". Click it to uncheck it. Then run your model. The resulting report should agree with R.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: estimates in multipule regression
Try this:
When filling in the Fit Model dialog, in the upper left corner of the dialog window there is a red triangle right next to the words "Model Specification". Click on that red triangle to bring up a context menu which includes as its first entry "Center Polynomials". Click it to uncheck it. Then run your model. The resulting report should agree with R.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: estimates in multipule regression
Hi abra,
Center Polynomials is the default option in JMP for situations in which you are fitting powers or interactions between variables, and for some good reasons. This process centers each variable (subtracts the mean from each observation) before operating on it (through powers or cross-products with other variables) so that the lower order terms are unconfounded with higher-order terms, and it also maintains an easy (and often more useful) interpretation of the coefficients: the "average" effect of a variable assuming other variables are held constant at their mean.
If you do not center variables, the interpretation of the lower order terms is different: the coefficients represent the increase in Y for each unit change of the variable when all other variables involved in higher-order terms with that variable are held constant at 0. This is why the test statistics and p-values for your X2 and X3 variables are different. The test of X2 in your model without centering is a test of the partial regression slope of Y|X2 when X3 is 0, and the test of X3 is a test of the partial regression slope of Y|X3 when X2 is 0. This happens because of that interaction term, which is capturing the degree to which the level of X2 affects the relationship between Y and X3, or alternatively and equivalently, the degree to which the level of X3 affects the relationship between Y and X2. All multiple regressions involve partial regression coefficients, which represent the effects of variables if we are to hold constant the levels of other variables. Where "constant" is, numerically, depends on that centering. With centering "constant" will be at the mean of other variables, otherwise "constant" will be at 0 of the other variables. (It's worth noting that without any interactions this choice is immaterial, since the slope of X2 and X3 are fit to be constant, thus their slopes are the same at 0 and the mean of the other variables, hence no effect of centering).
X1 is not involved in any higher order terms so the interpretation of it is unchanged by centering.
This is a great question and in the interest of making is as clear as possible I recorded a quick video using some of the profiling tools in JMP to drive home the main points and included it below.
I hope this helps!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: estimates in multipule regression
Great explanation on centering polynomials!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: estimates in multipule regression
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: estimates in multipule regression
Hi @Judd,
I've replaced the video - it seems that was lost at some point in the past.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: estimates in multipule regression
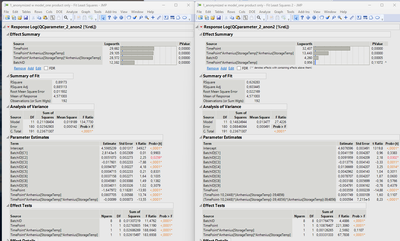
Probably a stupid question, but when I run the same model once without and once with "center polynomials" ticked, the report output looks totally different. I am trying to model relative degradation (t=0=100%) of a chemical compound over three different temperatures and in a multitude of different batches, following a recipe I received from a peer recently.
Copying the model windows to a script window shows that this is indeed the only difference. What am I missing?
Fit Model(
Y( Log( :"QCparameter_2_anon2 [%rel.]"n ) ),
Effects(
:BatchID, :TimePoint, :TimePoint * :"Arrhenius[StorageTemp]"n,
:TimePoint * :"Arrhenius[StorageTemp]"n * :"Arrhenius[StorageTemp]"n
),
Personality( "Standard Least Squares" ),
Emphasis( "Minimal Report" ),
Run(
:"QCparameter_2_anon2 [%rel.]"n << {Summary of Fit( 1 ),
Analysis of Variance( 1 ), Parameter Estimates( 1 ), Lack of Fit( 0 ),
Scaled Estimates( 0 ), Plot Actual by Predicted( 0 ), Plot Regression( 0 ),
Plot Residual by Predicted( 0 ), Plot Studentized Residuals( 0 ),
Plot Effect Leverage( 0 ), Plot Residual by Normal Quantiles( 0 ),
Box Cox Y Transformation( 0 )}
)
);
Fit Model(
Y( Log( :"QCparameter_2_anon2 [%rel.]"n ) ),
Effects(
:BatchID, :TimePoint, :TimePoint * :"Arrhenius[StorageTemp]"n,
:TimePoint * :"Arrhenius[StorageTemp]"n * :"Arrhenius[StorageTemp]"n
),
Center Polynomials( 0 ),
Personality( "Standard Least Squares" ),
Emphasis( "Minimal Report" ),
Run(
:"QCparameter_2_anon2 [%rel.]"n << {Summary of Fit( 1 ),
Analysis of Variance( 1 ), Parameter Estimates( 1 ), Lack of Fit( 0 ),
Scaled Estimates( 0 ), Plot Actual by Predicted( 0 ), Plot Regression( 0 ),
Plot Residual by Predicted( 0 ), Plot Studentized Residuals( 0 ),
Plot Effect Leverage( 0 ), Plot Residual by Normal Quantiles( 0 ),
Box Cox Y Transformation( 0 )}
)
);- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: estimates in multipule regression
Hi @Ressel : Why are you not including Arrhenius[StorageTemp] and Arrhenius[StorageTemp]^2 in your model?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: estimates in multipule regression
I am sheepishly, following a recipe. Below is a screenshot from a presentation I received and I am trying to replicate.
I was informed, that the below corresponds with a Taylor series, where TP = timepoint and Arrh(T) is the unspecific part of the Arrhenius equation per JMP documentation.
Question #1: Is this really a Taylor expansion?
Question #2: How many temperature settings do I need to use a 3rd degree Taylor expansion?
Question #3: Any hints on where to find literature that explains for dummies what the basic constraints and applications of the Taylor series in model fitting are?
Apologies for opening Pandora's box. (At the very least, people can now say that I had courage for exposing myself here.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: estimates in multipule regression
Hi @Ressel : This is the presentation I assume.
If you don't include the other terms I mentioned, then you have two different models...that is why the stat details are so different. It's easy to see if you expand out the centered factors, collect like-terms etc..
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us