- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: distribution of response variable
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
distribution of response variable
Hello:
I ran a DOE study of 5 factors.
It was a manufacturing process study and I measured the output which is the response variable.
for the identification of the significant factors and later forming a regression equation do we have to have the response variable following a normal distribution?
For my response variable for Normal distribution, AD is 0.886 and p-value is 0.18.
Should I go ahead with my DOE analysis on this response variable or should I first transform the response variable?
Your help is highly appreciated.
Best Regards,
Varun
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: distribution of response variable
Response variables do NOT need to be normally distributed. The RESIDUALS need to be normally distributed.
Think of it this way: Suppose Factor A is significant and has a large impact on the response, but none of the other factors are significant. Because Factor A has a large impact, the distribution of the response variable would likely be bi-modal. In other words, the distribution of the response variable should have signals in it. Therefore, you would not expect it to be normally distributed.
Once you have done your modeling, you should explain all of the signals in the data. All that is left (residuals or error) should follow the normal distribution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: distribution of response variable
The questions are getting a bit more difficult now, especially without seeing the plots, data, or knowing the context. So others may disagree with my responses.
First, a U-shaped pattern typically would indicate curvature, not unequal variance. If there is curvature present, perhaps adding quadratic terms to the model would resolve the issue.
But to try to answer your questions about unequal variance:
1) Yes, equal variance is still important. It is an assumption for a reason. When any test is performed on a parameter estimate, there is only one estimate of error being used. But if the variance is changing, then the single error estimate that is used is not really accurate. All of the testing could be suspect. Think of it this way: I have data points of 10, 20, 30, and 2000. The average is 515. Is that an adequate representative value of the data? Probably not. Now imagine that those four numbers are the variances at different points across the range of predicted values. The 515 would represent the single error number being used for the testing. It likely would not be appropriate for all of the testing.
2) See answer #1. Equal variance is important. It might be less important when screening, but it will depend on what you are using to do the screening. Statistical testing will be more suspect. Some of the graphical techniques might be more appropriate. However, by not addressing the unequal variance problem you may still be missing some important factors or be misled into thinking some are important when they are not.
3) There are some standard transformations that can be applied, but there is no guarantee that any of them will work. Standard transformations are log, reciprocal, square root, squaring, or exponentiation. You could even use Box-Cox transformation. Another approach is to switch away from standard least squares regression and use a general linear model that will allow you to explicitly model the error term.
4) There are some tests that could be performed to check for equal variances. In my opinion (others may disagree -- and if so, please chime in!), those tests are not worth the effort. If you look at the plots and say that the variance is changing, then I would believe it is.
Remember that statistical tests are a tool for you to make the decision, they do not make the decisions for you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: distribution of response variable
From your plots I see a definite "U" shaped pattern on the residuals versus predicted values. That indicates that you have curvature. You can also see this with the bimodal histogram of the residuals. I would invest in adding additional experiments to allow the modeling of quadratic terms. (the data currently does not support a higher order model). Adding additional experiments and fitting a higher order model will likely resolve the pattern in the residuals.
Results like this are not uncommon in a screening design. I would recommend resolving the patterns seen in the residuals before worrying about the variance of the residuals. In fact, I do not really see a changing variance in the residuals. A changing variance pattern would look like a "fanning out" of the residuals (higher variance on the right or left-side of the plots).
But if you still think there is a variance issue, then resolving the pattern may improve the potential variance problem. Transforming the response is typically the LAST thing that is done (and only if necessary) unless there is some underlying scientific reason to perform the transformation.
Disclaimer: Oh, and I think that you should get a copy of JMP. :)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: distribution of response variable
update:
For my response variable for Normal distribution, AD is 0.886 and p-value is 0.018
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: distribution of response variable
Response variables do NOT need to be normally distributed. The RESIDUALS need to be normally distributed.
Think of it this way: Suppose Factor A is significant and has a large impact on the response, but none of the other factors are significant. Because Factor A has a large impact, the distribution of the response variable would likely be bi-modal. In other words, the distribution of the response variable should have signals in it. Therefore, you would not expect it to be normally distributed.
Once you have done your modeling, you should explain all of the signals in the data. All that is left (residuals or error) should follow the normal distribution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: distribution of response variable
Thank you Dan:
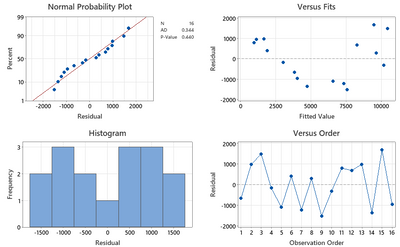
The residuals in my case are normally distributed with AD of 0.344 and p-value of 0.440
I was also checking for the equal variance of the residuals, I plotted Residual vs Fitted value and see a U-shaped pattern.
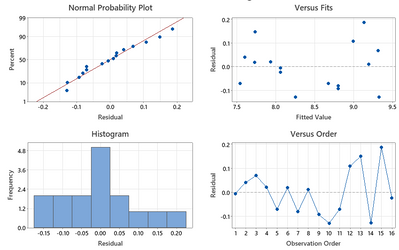
when I do a logarithmic transformation of the response variable, I see somewhat better dispersion of data points
My question is:
Q1) Is equal variance in residuals important, if we have normally distributed residuals?
Q2) Is equal variance in residuals important, if we only want to screen the factors and no regression equation is needed?
Q3) Is there a guideline to see what transformation should be done on the response variable?
Q4) Is there are a way (other than observing it) to say that the residuals have acceptable variation?
Your help is highly appreciated.
Best Regards,
Varun
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: distribution of response variable
The questions are getting a bit more difficult now, especially without seeing the plots, data, or knowing the context. So others may disagree with my responses.
First, a U-shaped pattern typically would indicate curvature, not unequal variance. If there is curvature present, perhaps adding quadratic terms to the model would resolve the issue.
But to try to answer your questions about unequal variance:
1) Yes, equal variance is still important. It is an assumption for a reason. When any test is performed on a parameter estimate, there is only one estimate of error being used. But if the variance is changing, then the single error estimate that is used is not really accurate. All of the testing could be suspect. Think of it this way: I have data points of 10, 20, 30, and 2000. The average is 515. Is that an adequate representative value of the data? Probably not. Now imagine that those four numbers are the variances at different points across the range of predicted values. The 515 would represent the single error number being used for the testing. It likely would not be appropriate for all of the testing.
2) See answer #1. Equal variance is important. It might be less important when screening, but it will depend on what you are using to do the screening. Statistical testing will be more suspect. Some of the graphical techniques might be more appropriate. However, by not addressing the unequal variance problem you may still be missing some important factors or be misled into thinking some are important when they are not.
3) There are some standard transformations that can be applied, but there is no guarantee that any of them will work. Standard transformations are log, reciprocal, square root, squaring, or exponentiation. You could even use Box-Cox transformation. Another approach is to switch away from standard least squares regression and use a general linear model that will allow you to explicitly model the error term.
4) There are some tests that could be performed to check for equal variances. In my opinion (others may disagree -- and if so, please chime in!), those tests are not worth the effort. If you look at the plots and say that the variance is changing, then I would believe it is.
Remember that statistical tests are a tool for you to make the decision, they do not make the decisions for you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: distribution of response variable
Thank you very much for the detailed response, Dan.
This is highly appreciated.
Below is the data.
B is categorical and rest all are continuous.
| Blocks | A | B | C | D | E | response | ln(response) |
| 2 | 14.78 | Yes | 3 | 60 | 20 | 3152 | 8.055792451 |
| 2 | 11.48 | No | 3 | 20 | 60 | 2090 | 7.644919345 |
| 2 | 14.78 | Yes | 10 | 60 | 60 | 11920 | 9.385972941 |
| 2 | 14.78 | No | 3 | 20 | 20 | 2856 | 7.957177323 |
| 2 | 11.48 | No | 10 | 20 | 20 | 5472 | 8.607399459 |
| 2 | 11.48 | Yes | 3 | 60 | 60 | 2314 | 7.746732908 |
| 2 | 11.48 | Yes | 10 | 60 | 20 | 6133 | 8.721439306 |
| 2 | 14.78 | No | 10 | 20 | 60 | 9930 | 9.203315757 |
| 1 | 11.48 | Yes | 10 | 20 | 60 | 6058 | 8.709134992 |
| 1 | 14.78 | No | 10 | 60 | 20 | 9883 | 9.198571388 |
| 1 | 11.48 | Yes | 3 | 20 | 20 | 1765 | 7.475905969 |
| 1 | 11.48 | No | 10 | 60 | 60 | 8972 | 9.101863896 |
| 1 | 11.48 | No | 3 | 60 | 20 | 2662 | 7.886832999 |
| 1 | 14.78 | No | 3 | 60 | 60 | 3381 | 8.125926803 |
| 1 | 14.78 | Yes | 10 | 20 | 20 | 11170 | 9.320986892 |
| 1 | 14.78 | Yes | 3 | 20 | 60 | 3093 | 8.0369 |
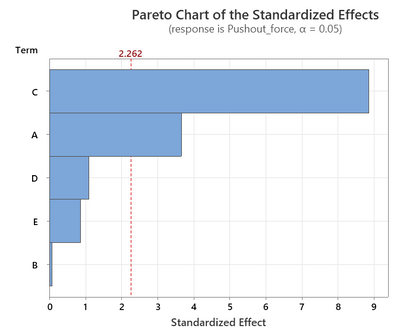
Below are the residual plots for response (If I analyze the response factor A and C are significant)
only analyzing Main effects
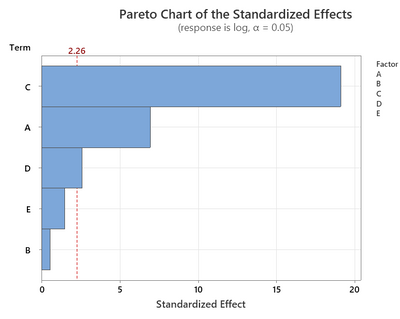
Now if I take the natural log of response and analyze the data, I get below shown residual plots.
It seems that the residual vs fitted is better in this and factor D also becomes significant.
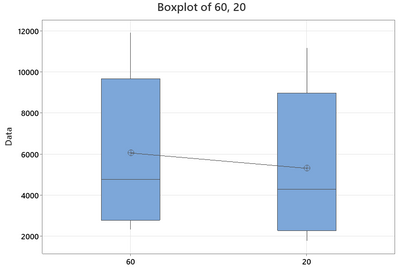
When I do a box-plot of response (not the ln-response) with respect to factor D, the variance is pretty much the same as shown below.
My question is:
Q1) Is transformation needed?
Q2) Should I do the transformation?
Q3) Does response variance with respect to factor D play any significance in the decision of transformation?
Your help is highly appreciated.
Best regards,
Varun
Disclaimer: I have access to JMP software through a Coursera course that I enrolled, but I can only do a study related analysis. Since this project is industrial, I am doing it in Minitab.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: distribution of response variable
From your plots I see a definite "U" shaped pattern on the residuals versus predicted values. That indicates that you have curvature. You can also see this with the bimodal histogram of the residuals. I would invest in adding additional experiments to allow the modeling of quadratic terms. (the data currently does not support a higher order model). Adding additional experiments and fitting a higher order model will likely resolve the pattern in the residuals.
Results like this are not uncommon in a screening design. I would recommend resolving the patterns seen in the residuals before worrying about the variance of the residuals. In fact, I do not really see a changing variance in the residuals. A changing variance pattern would look like a "fanning out" of the residuals (higher variance on the right or left-side of the plots).
But if you still think there is a variance issue, then resolving the pattern may improve the potential variance problem. Transforming the response is typically the LAST thing that is done (and only if necessary) unless there is some underlying scientific reason to perform the transformation.
Disclaimer: Oh, and I think that you should get a copy of JMP. :)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: distribution of response variable
Thank you very much for your detailed explanation, Dan.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us