confidence interval

[#1]

How do I display a confidence interval in an exponential curve. I figured it out for a linear but not for an exponential curve. Thanks!

[#2]

Hi @AdditivePony307 : When you say "exponential" what exactly do you mean?

1. Something like this: Y=A*exp(k*x)

2. Something like this: Y = A*(1-exp(k*x))

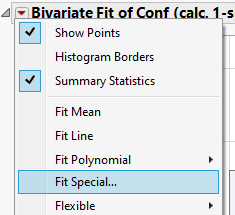
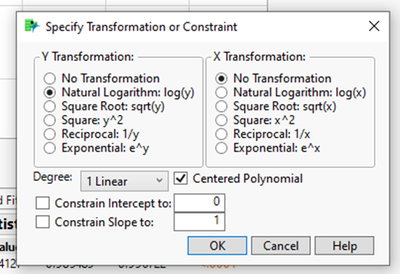
If (1), then you can use Fit Y by X. Then choose "Fit Special..." and choose Natural Log under Y transformation (see screen shots below). If more like (2) the you will have to go through the non-linear platform. If (1) via below, then the "intercept" in the Parameter Estimates output is ln[A] (so A = exp[intercept] ) , and "X" (whatever your X is) is k.  

[#3]

Thanks for your reply!

My curve fit looks like this:

DOC(t) = DOC∞ + z0 -kt

it describes microbial drawdown of dissolved organic carbon (DOC) in water over time (t) in a bioassay.  This is part of a paper and the reviewer suggested to add the confidence area. Do you have an idea how? 

[#4]

Here is the correct formula:

DOC(t) = DOC∞ + z0 * exp(-kt)

[#5]

Hi @AdditivePony307 : OK, you will have to go through the Non Linear Platform; I'm assuming DOC-inf, z0, and k are parameters to be estimated via the regression. See this and come back if needed.

https://www.jmp.com/support/help/en/17.2/index.shtml#page/jmp/example-of-the-nonlinear-platform.shtm...

[#6]

Ok, thanks!