- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- clopper-pearson confidence interval for proportion
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
clopper-pearson confidence interval for proportion
Hi group!
is there functionality in JMP 11 for calculation of Clopper-Pearson exact confidence intervals for a proportion?
If I am not wrong, the manual only mentions this method for sample size calculations.
Thanks,
Dave
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: clopper-pearson confidence interval for proportion
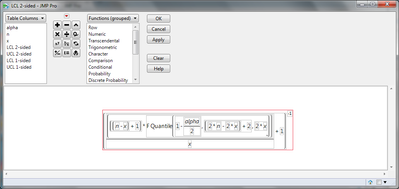
You can build the formulas in JMP for upper and lower confidence limits (2-sided or 1-sided) following Hahn and Meeker's book Statistical Intervals sections 6.2.2 and 6.2.5. Very useful book.
Lower 2-sided 100(1-alpha)% confidence limit for p = x/n:
Upper 2-sided 100(1-alpha)% confidence limit for p = x/n:
For 1-sided limits replace alpha/2 by alpha.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: clopper-pearson confidence interval for proportion
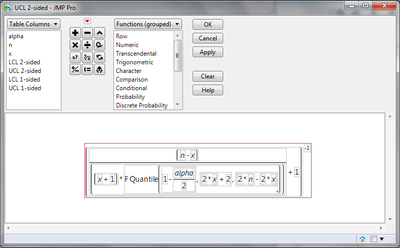
You can build the formulas in JMP for upper and lower confidence limits (2-sided or 1-sided) following Hahn and Meeker's book Statistical Intervals sections 6.2.2 and 6.2.5. Very useful book.
Lower 2-sided 100(1-alpha)% confidence limit for p = x/n:
Upper 2-sided 100(1-alpha)% confidence limit for p = x/n:
For 1-sided limits replace alpha/2 by alpha.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: clopper-pearson confidence interval for proportion
This is probably going to open a can of worms, but that's never stopped me before...
The Clopper-Pearson confidence intervals have been shown (Agresti, A. and Coull, B.A.(1998); "Approximate is Better Than Exact for Interval Estimation of Binomial Proportions"; The American Statistician Vol. 52 No .2; pp. 119-126) to have coverage probabilities that are overly conservative, especially in the tails.
That paper recommends Wilson Score Intervals, which are calculated natively in JMP in the Distribution platform. Since I usually find myself thinking about "average" coverage performance of confidence intervals, and not "worst-possible" coverage performance, I tend to prefer the Wilson Score CI's.
Clopper-Pearson is the historical "gold standard", but I recommend you cast off the yoke of convention and go Wilson Score. Plus, no formulae are required.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: clopper-pearson confidence interval for proportion
Dear Kevin,
thanks for your suggestion. I have calculated Wilson Score CI's previously, but sometimes it is a matter of who is to review the information and their preferences. Such is the case of some regulatory bodies, and, unfortunately, I am in no position to argue.
Best,
Dave
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: clopper-pearson confidence interval for proportion
Note that the solution already covered uses the Fisher-Snedecor distribution (aka F-distribution), which is perfectly appropriate and highly accurate to approximate the binomial. Here is an additional publication reference which details the calculations for Clopper-Pearson and includes another method (using the Beta Equation, from p. 38 of Krishnamoorthy, K., Handbook of statistical distributions with applications, (c) 2006 Chapman& Hall, CRC Press) which works equally well.
LCL =
UCL =
where C = confidence desired or required, k = number observed events, and N = total number of possible events.
https://www.johnzorich.com/s/Reasons-for-Using-the-Coefficient-of-Determination-by-John-Zorich.pdf
(Example attached in JMP).
Also, good dialog from @Kevin_Anderson and reply from @david_arteta: I hadn't thought about the Score CIs in terms of their propensity to handle "average" coverage performance -- (this is likely whey JMP adopted them since most users are probably concerned about the "on average" performance in their science or engineering work). From my experience working in industries with regulatory oversight by FDA and other European Notified Bodies -- the "worst case" coverage performance seems to be generally preferred and for this reason I think the "Clopper-Pearson" is the required choice. Basically as @david_arteta said, we aren't in a position to argue there.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us