- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Why are my predicted values for my model (ZI negative binomial) all the same?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Why are my predicted values for my model (ZI negative binomial) all the same?
So, I've got a number of zero-inflated negative binomial models and I want to graph them so I've been saving the predicted values. For the models that don't have any significant factors though, the values are all the same. Why is this? Shouldn't there still be at least some sort of trend, even if it's not significant? Similary, one of my models had a significant interaction (between my blocking factor and my main continuous factor). One of the blocks has all of the same values while the other block exhibits a trend.
Why am I seeing this?
Edit: Also, it seems like all my metrics have the same exact trend. While I know that's not completely impossible, it seems strange that they're almost all exactly the same. Does this have something to do with me using a negative binomial distribution?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why are my predicted values for my model (ZI negative binomial) all the same?
Bump.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why are my predicted values for my model (ZI negative binomial) all the same?
Anyone? Sorry for the incessant replies. A lot of my analyses for my thesis depend on this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why are my predicted values for my model (ZI negative binomial) all the same?
Which models? Are they distribution models, such as used by Life Distribution? Are they mean response models, such as used by Generalized Regression?
You want to plot them? Save the model as a column formula and then use Graph Builder. It will plot the graph of a function.
The model for the mean response will be a constant if there are no significant independent variables / factors / predictors / features (intercept only).
If you have an interaction effect, then by definition the effect of one factor (e.g., block) depends on the level of another factor (e.g., continuous factor). (BTW, are you sure you want to model such an interaction? Generally, we do not model interactions with blocking factors for philosophical and realistic reasons.)
Can you share the design, data, and output that you are asking about? I have a vivid imagination, but it isn't that good.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why are my predicted values for my model (ZI negative binomial) all the same?
Hi Mark,
Thanks for the reply. I'm running mean response models. One set of data is run as a zero-inflated negative binomial model and the other set of data is run as a negative binomial model.
Forgive my ignorance (I'm not nearly as familiar with negative binomials and the generalized regression tool in JMP as I'd like to be) but why does the model for the mean response only provide a constant for predicted values when there aren't any significant factors? Even if a model isn't significant, there could still possibly be a trend which is something that I'd definitely be interested in seeing. Is this a limitation of the generalized regression tool in JMP?
Using the "Save Prediction Formula" function has primarily been how I've been graphing my models. That's where I've been seeing these constants for my predicted values in non-significant models.
Quick rundown of my design is a continuous predictor (sex ratio) with a blocking factor. I'm looking at how my predictor impacts the reproductive output of a fish species. When I run my model I'm using sex ratio, the blocking factor, and the interaction between the two. Additionally, I've included the average size of male and female individuals on my reefs (my replicates) as covariates. I used Forward Selection and AICc for model fitting.
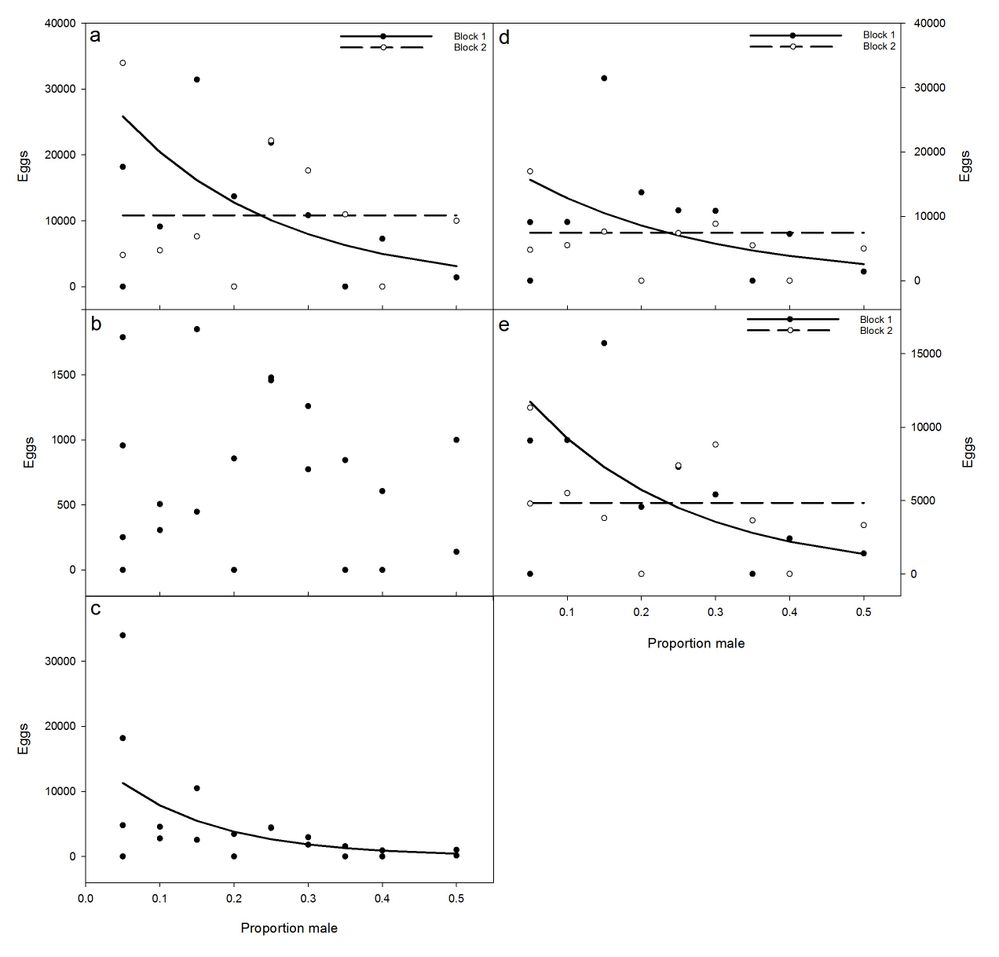
I've included an example of the outputs of one of my models (this particular model is looking at the total production on individual reefs). I've also included a panel of my results for this particular model; figure A is the panel that pertains to this analysis. The figures were made in SigmaPlot but were made using the predicted values from my JMP analyses.
I definitely understand the argument for not modeling interactions with blocking factors. For whatever reason though, in my field (marine ecology), it's very common so it'd be unusual if I didn't.
Thanks for the reply Mark and any help is greatly appreciated. Let me know if you would like to see more outputs and/or clarification.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why are my predicted values for my model (ZI negative binomial) all the same?
It is not a limitation of the generalized regression in JMP. The plot shows the graph of the function that you used as a model for the mean response. It generally looks something like this in the absence of significant factors: Y = B. B is the constant term, or intercept. Why would you expect the predicted mean to show a trend when the prediction is always B?
I see that your response is total counts. The negative binomial distribution model generally applies to a series of independent Bernoulli trials. It models the number of successes in a sequence of independent and identically distributed Bernoulli trials before a specified (non-random) number of failures occurs. What is the definition of a success and a failure in your situation? Count data are generally modelled better with a Poisson distribution, which has appropriate assumptions. This single parameter model can be augmented with an over-dispersion parameter and you can include a log offset if your area of opportunity is not constant.
What is the definition of a block in your situation? How many blocks occurred in your study?
What is the significance of a through e in the series of plots?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why are my predicted values for my model (ZI negative binomial) all the same?
You're right. I think I was assuming that the mean response would be based off of my observed values rather than my predicted values (despite saving my "Prediction foruma". Doh). In hindsight, I see why I'm getting constant values when my response is the intercept. The vast majority of my work up until this point has been dealing with normal distributions and I guess I was trying to use the predicted values to fit a line to my observed values as best I could (similar to a linear regression). I'm sure I'm still miscontruing a lot of this but I'm beginning to see why I have problems.
My response is indeed total count (of eggs). While I had originally used a Poisson model before, people had recommended using a negative binomial distribution since it appears that I'm dealing with overdispersion. I wouldn't necessarily say I have a definition of success or failure in my model. Unless the presence of eggs was considered a "success" although that's ultimately not really what I'm interested in. So, I'm sure you're right that I should likely be using a Poisson distribution. Is it possible to apply a overdispersion parameter to a Poisson model in JMP? Would you mind clarifying what you mean by "area of opportunity".
A block in my situation has a single replicate of all of my treatments within it (randomized) in an attempt to deal with spatial heterogeneity. Unfortunately, I only had two blocks in my model (was limited by space and funding).
Plots A through E in my panel represent the 5 different metrics that I'm looking at: total egg count (per reef), female per capita, male per capita, egg production per nest, and egg production per clutch. Essentially they're all different ways of looking at reproductive output in my species. Plots with a trend line are significant. Plots A, D, and E all had a signficant interaction (sex ratio * block; proportion male and sex ratio are used interchangeably in my study) but nothing else after selection. Just sex ratio was significant for Plot C. The scale of the response differs but in all 5 plots it's egg count.
Really, really appreciate all of your input so far Mark. Your replies have cleared up a lot of things for me. Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why are my predicted values for my model (ZI negative binomial) all the same?
A negative binomial distribution model is, in fact, useful when there is over-dispersion, but every model has a purpose and a set of assumptions. A Bernoulli trial has two outcomes and you need to observe both outcomes. If you consider an egg as a success, then how do you count the failure (non-egg)?
You can use a Poisson distribution model with an over-dispersion parameter, so you do not lose the flexibility of the negative binomial distribution model. You gain the benefit of a model with assumptions that match your situation.
The area of opportunity is a central concept of the counting process. For example, I might count the number of accidents weekly on a specific highway, in which case a week is the area of opportunity. I might count the number of Staphylococcus infections per 100 hospital beds in the surgical department, in which case 100 beds is the area of opportunity. These are examples where the area of opportunity remains constant while I model counts or test for changes. On the other hand, if I counted the number of accidents on many different highways (different length, different kinds of traffic and traffic loads) or I counted the number of Staphylococcus infections occurring in many different hospitals (different number of beds, different departments and specialities), then the area of opportunity for each count varies. I need to measure the area of opportunity and add it to the Poisson log linear model as the log offset. You say that you count eggs per reef. Is every reef included in the study afford the same area of opportunity? If not, how do you determine their different areas of opportunity?
I am still not clear about what you mean by a block. Is it simply a replicate of the entire design? If so, then an interaction effect really means that there is a lurking variable or hidden factor at work, not just a random effect (replicate variance). How do I get another block or make another block in your situation? I assume that by "spatial heterogeneity" you are referring to differences among reefs. But isn't that just your random error (sampling error)? If so, then you should not model it as a fixed effect (interaction).
After we sort out some of these details, we can discuss the plots.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why are my predicted values for my model (ZI negative binomial) all the same?
Thanks for the reply Mark.
The more we talk about it, the more I'm thinking a Poisson with an overdispersion parameter would be the appropriate model. I would not consider my response to be a Bernoulli trial. I'm not concerned with success/failure (i.e., eggs/no eggs) but with the number of eggs in each treatment. How would I go about adding a overdispersion parameter to a Poisson model in JMP? I don't see an option in the Generalized Regression Personality. Would it be somewhere in the Generalized Linear Model personality?
Thanks for the clarification on area of opportunity. The area of opportunity is consistent throughout the study. Reefs are all the same size with the same number of nests. All of the nests are the same size as well.
My experimental design incorporated blocks to deal with spatial heterogeneity in the environment. Blocks were set up during the field manipulation portion of the study; they aren't something that I can add at this point (although I can remove them from my analyses of course). One block contains a single replicate of each treatment. I have 10 different treatments (i.e., sex ratios); each reef has a single treatment/sex ratio. Each block has 10 reefs (i.e. 10 treatments). I have 2 blocks and 20 reefs total. If you look at the plots you can see that at each different sex ratio there is a reef from block 1 and a reef from block 2.
You're right that a significant interaction between my main predictor and my blocks means that there is some lurking variable at work...and we don't necessarily know what it is. I'd argue that field manipulations in marine ecology are notoriously noisy. Blocking is one way that we try to minimize that noise.
Hope that starts to clear things up. Thanks a bunch. Appreciate it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why are my predicted values for my model (ZI negative binomial) all the same?
I will study your explanation of blocks later. For now, I will just answer the question about the fitting personality.
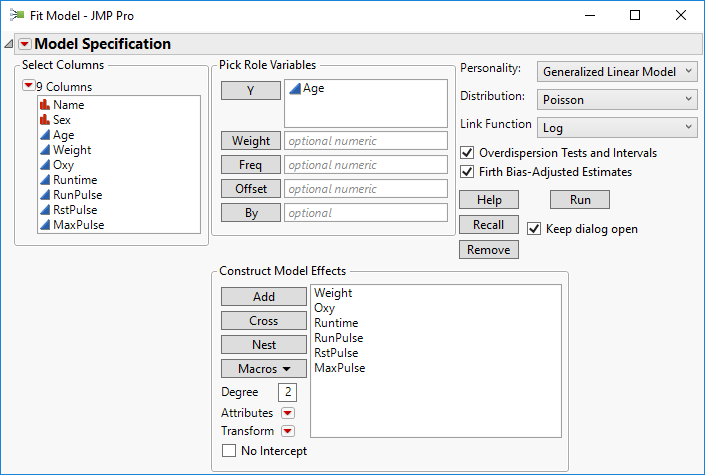
I can't find an over-dispersion option in Generalized Regression either, but I was in a hurry. It is available in the Generalized Linear Models personality:
Note the selections in the upper left corner of the dialog box.
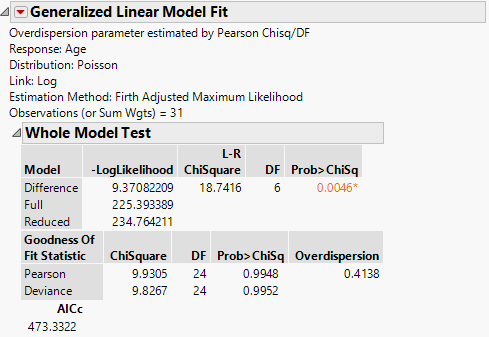
The results of running the model include information about the need for over-dispersion (test) and the estimate of the parameter:
The Pearson Chi square in the Goodness of Fit report is the test and the parameter estimate is to the far right.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us