- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- What to do with potentially Cauchy distribution of residuals (%growth data, incl...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
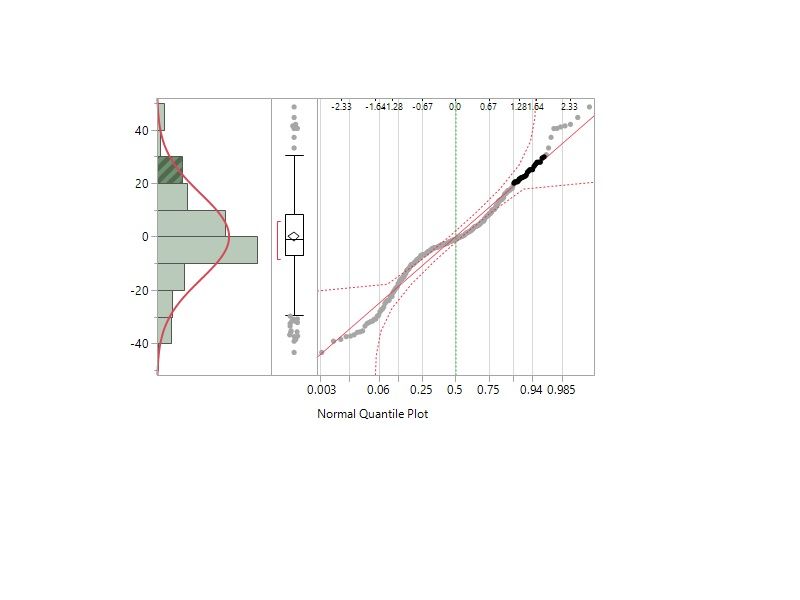
What to do with potentially Cauchy distribution of residuals (%growth data, including some negative)
Hi, I am trying to run an ANOVA on a complex data set.
Long story short, there are 4 fixed factors (a,b,c,d), and one random factor
factor c is nested within b
The data are percentage growth, like this: [(final-initial)/final]*100
Some individuals shrunk (they are mussels and are known to do this), so I have negative values and some grew 100% (ie they are not bound by 0 and 100)
My residuals are not normally distributed, nor do they have equal variances.
In asking around, it seems the residuals may be cauchy distributed.
I have found that cauchy distribution means you can't do regular ANOVA. Does anyone have any tips?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What to do with potentially Cauchy distribution of residuals (%growth data, including some negat
For starters the first thing I would evaluate is how does this apparent collection of non-normally distributed errors affect the practical questions your trying to address with the experiment? I encourage you to think about the practical questions first, then let the statistics (of which the distributional shape of the residuals is but one) guide you. If you've successfully answered the pratical questions that are being posed, and the magintude of the residuals is not problematic from a decision making point of view...well who cares if they are not normally distributed?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What to do with potentially Cauchy distribution of residuals (%growth data, including some negat
For starters the first thing I would evaluate is how does this apparent collection of non-normally distributed errors affect the practical questions your trying to address with the experiment? I encourage you to think about the practical questions first, then let the statistics (of which the distributional shape of the residuals is but one) guide you. If you've successfully answered the pratical questions that are being posed, and the magintude of the residuals is not problematic from a decision making point of view...well who cares if they are not normally distributed?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What to do with potentially Cauchy distribution of residuals (%growth data, including some negat
Thank you for this. My advisor told me pretty much the same thing, but he's not stats-minded at all. This feels like going to the doctor to get a second opinion. Overall the data show a pretty blatant effect of the treatments, but not analyzing them in the exact proper method was like having a puzzle where you know what the image is, but not having all the pieces and refusing to put it down. Thanks again.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us