- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: What to do with contained effects
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
What to do with contained effects
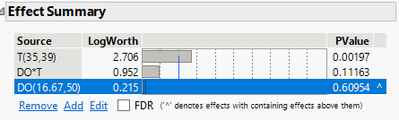
I am running a 2x2 full factorial study and only looking to model main effects and one-way interactions. As shown below, I have a main effect that appears as less significant than the one-way interaction that contains it. I know the interaction factor is also itself insignificant, but in the past I've seen it as significant. In the past i've just removed the insignificant interaction factor before removing the main effect. Is there any guidance on this? Why might this happen? Is there anything specifically in the dataset that causes this? What is the proper way to handle effects in the situation? Thanks in advance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What to do with contained effects
JMP respects 'model heredity.' This principle states that you should include lower-order terms, even if they are not significant if you include higher-order terms that contain them. It is not about the physical science underlying the response or a theoretical model. Experimenters generally expect the model to be scale invariant. That is to say that if I change the scale for a factor, the terms in the model remain the same. That is not the case if you do not respect model heredity. JMP follows the best practice of coding all the factor levels to [-1,1]. The coefficients are, therefore, coded as well. You might convert the model to the original scientific or engineering scale. You would observe changes in the terms if you disregard model heredity.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What to do with contained effects
@Mark_Bailey , I thought this was the hierarchy principle. That is, following the principle of hierarchy, if you have a 2nd order (higher order) effect, you should include the first order (lower order) effects. Heredity is an analysis principle that may help determine which of confounded higher order effects are active by assessing the significance of the lower order effects. Heredity: In order for a higher order effect to be active, at least 1 parent should be active. Correct me if I am wrong.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What to do with contained effects
I understand that these terms have been swapped here and elsewhere in the past. I am using the terms as JMP would.
Effect hierarchy is the often observed principle that most effects are first-order, the next largest effects are second-order, and so on. Third-order effects are rather rare.
We use model heredity to mean that higher-order terms (predictor linear combination) should include lower-order terms
I don't think you are wrong. My use is merely consistent with JMP. We all have to be careful to explain what we mean when we use certain terms. You always explain yourself.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What to do with contained effects
Hello @sanch1,
about the interaction showing up as active when you believe it should not, have you tried to plot an interaction plot with all data points to unerstand why the interaction is showing up as active? In the article Søren Bisgaard & Michael Sutherland (2003) Split Plot Experiments:Taguchi's Ina Tile Experiment Reanalyzed, Quality Engineering, 16:1, 157-164), the authors show an example of this this plot with this situation for a unreplicated experiment. Problems in your data acquisition or some error on recording the data into the table might cause this effect.
Emmanuel
========================
Keep It Simple and Sequential
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What to do with contained effects
In a 2x2 full factorial study, it's common to find that the significance of main effects and interactions can vary based on factors and interactions between them. Sometimes, a main effect might appear less dg dollar general significant compared to an interaction that includes it, possibly due to the combined impact of multiple factors. When faced with an interaction that contains a less significant main effect, consider simplifying your model by removing non-meaningful terms to focus on more interpretable effects.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What to do with contained effects
Hi @sanch1,
The statistical explanation by @Mark_Bailey can help you understand how/why model heredity is used to build models based on DoE data. I would like to provide further questions and remarks on the modeling and significance of effects :
- Take into consideration there are possibly many ways to get to different (yet useful) models, depending on your evaluation metric for "significance" or model "accuracy" : p-value threshold for effects, information criterion like AICc and BIC, R²/R² adjusted, RMSE, ... What is important is to use the metric(s) aligned with your goal and objective (explanative and/or predictive model).
- Concerning your questions, I would also emphasize the need to differentiate statistical significance from practical significance (size effect). See more info on this previous topic : https://community.jmp.com/t5/Discussions/Which-one-to-define-effect-size-Logworth-or-Scaled-Estimate...
Depending on your signal-to-noise ratio, you might be able to statistically detect (or not) some main effects and/or interaction effects. In a "controlled" environment (where nuisance factors are "controlled" or maintained), with possibly high precision measurement system (with high repeatability and reproducibility accuracy), you might be able to detect effects with very small effect size. Depending on the conditions in which you have done previous studies, that may explain why you may have missed those effects. - The experimental space and sample size may also be different between your earlier studies and this study done with DoE. Depending on the factors, factors ranges, assumed model and repartition of point in the experimental space, you might have differences in the representativeness of your dataset and the ability to detect effects. For example, a very narrow space with low sample size make the detection of statistically significant effect more difficult. Related to the point 2, very large samples tend to transform small differences into statistically significant differences, so this is why practical significance is needed to assess the model adequacy.
It's important to complement statistical analysis with domain expertise to challenge/inform the model(s) you have created and use validation runs to confirm your final model's predictions.
I hope these (not exhaustive) considerations may help you understand the differences you have seen in your different analysis,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us